Exercícios de Partícula na Caixa Unidimensional - Lista de Exercícios Resolvida

Um elétron que está confinado em um poço de potencial infinito unidimensional de largura é excitado do estado fundamental para o primeiro estado excitado.

Essa excitação aumenta, diminui ou não tem nenhum efeito sobre a probabilidade de detectar o elétron em uma pequena região:

1. No centro do poço?
2. Perto de uma das bordas do poço?

Seja a diferença de energia entre dois níveis de energia adjacentes e para uma partícula em uma caixa (poço infinito). A razão compara a energia de um nível com a diferença de energia entre este nível de energia e a energia de um nível adjacente.

Qual é o valor máximo de ?

Nenhuma das anteriores.

1. Determine o nível de energia mais baixo para a partícula em uma caixa supondo que a partícula seja uma bola de bilhar e que a largura da caixa seja , o tamanho de uma mesa do jogo de bilhar. (Suponha que a bola de bilhar deslize sem atrito em vez de rolar. Ou seja, despreze a energia cinética da rotação.).
2. Como a energia do item (a) é totalmente dada pela energia cinética, a que velocidade isso corresponde? Com essa velocidade, quanto tempo a bola levaria para ir de uma extremidade da mesa até a outra?
3. Qual é a diferença de energia entre os níveis e ?
4. Os efeitos da mecânica quântica são importantes para o jogo de bilhar?

Um próton é confinado em um poço de potencial infinito unidimensional com de largura.

Qual é a energia do estado fundamental?

Dado:

Massa do próton

Uma partícula de massa está confinada em um tubo de comprimento .

O momento linear e a energia dessa partícula são respectivamente iguais a:

É necessário fornecer de energia a um átomo para excitar um elétron do nível fundamental até o primeiro nível excitado.

Considere o átomo um elétron em uma caixa e calcule a largura da caixa.

Dado:

Massa do elétron

Um elétron está confinado em um poço de potencial infinito unidimensional com de largura; o elétron se encontra no estado fundamental.

Qual é a probabilidade de que o elétron seja detectado em uma região de largura em torno do ponto:

(Sugestão: A largura é tão pequena que a densidade de probabilidade pode ser considerada constante em seu interior)

Um elétron encontra-se aprisionado num poço de potencial unidimensional infinito de comprimento (caixa quântica).

Este elétron comporta-se como uma corda presa nas extremidades e e está inicialmente no estado fundamental.

Dados , , e , em função dos dados:

1. Deduza a energia e o momento do elétron.
2. Encontre o vetor de estado (função de onda) para o estado fundamental, normalizado.
3. Qual a probabilidade de encontrar o elétron entre e , se ele estiver no segundo estado?
4. Se o elétron estiver no quarto estado, quais os pontos de menor probabilidade de encontrar o elétron, em função de ?
5. Se o elétron estiver no quarto estado, quais os pontos de maior probabilidade de encontrar o elétron, em função de ?

Seja a diferença de energia entre dois níveis de energia adjacentes e para uma partícula em uma caixa (poço infinito). A razão compara a energia de um nível com a diferença de energia entre este nível de energia e a energia de um nível adjacente.

Qual é o valor máximo de ?

Nenhuma das anteriores.

Uma partícula de massa m está confinada em um poço de potencial infinito (“caixa unidimensional”), tal que

(a) A partir da equação de Schrödinger, verifique que é uma função de onda possível para representar o estado quântico dessa partícula e, com isso, encontre a energia associada a esse estado.

(b) Encontre o valor esperado da posição da partícula no estado do item (a).

Faça a escolha correta e justifique:

A energia no estado 𝑛=2 de um elétron confinado em uma caixa unidimensional de comprimento 𝐿 = 0,1 𝑛𝑚 é:

(a ) 3,79 eV

(b ) 74,5 eV

(c ) 206 eV

(d ) 151 eV.

Um elétron encontra-se aprisionado num poço de potencial unidimensional infinito de comprimento (caixa quântica).

Este elétron comporta-se como uma corda presa nas extremidades e e está inicialmente no estado fundamental.

Dados , , e , em função dos dados:

1. Deduza a energia e o momento do elétron.
2. Encontre o vetor de estado (função de onda) para o estado fundamental, normalizado.
3. Qual a probabilidade de encontrar o elétron entre e , se ele estiver no segundo estado?
4. Se o elétron estiver no quarto estado, quais os pontos de menor probabilidade de encontrar o elétron, em função de ?
5. Se o elétron estiver no quarto estado, quais os pontos de maior probabilidade de encontrar o elétron, em função de ?

Considere uma caixa quântica, também chamada de poço de potencial infinito, unidimensional, onde a função energia potencial é muito grande (infinita) nos ponto e , é nula para (região ), nula para (região ), e novamente nula para (região .

Para um objeto quântico dentro da caixa, teremos uma possível função de onda dada por (obs: e são constantes):

; ;

; ;

; ;

; ;

; ;

Nenhuma das anteriores

Considere uma partícula de massa e energia num potencial unidimensional que é nulo na região e infinito para ou .

1. Escreva a função de onda nas regiões e . Justifique.
2. Escreva a equação de Schrödinger independente do tempo na região e as condições de contorno que a função de onda deve satisfazer.
3. Resolva a equação de Schrödinger com as condições de contorno, determinando as funções de onda (não é necessário normalizá-las) e os níveis de energia.

A dinâmica de uma partícula subatômica de massa pode ser estudada modelando-a confinada em um poço unidimensional de largura como mostra a figura.

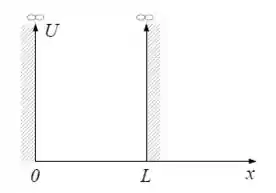
1. Escreva a equação de Schrödinger para esta partícula com energia no poço.
2. Obtenha, resolvendo a equação do item , as funções de onda normalizadas .
3. Qual é a separação em energia entre os estados da partícula correspondentes aos dois níveis mais baixos de energia nesse poço?

. PARTE 2

Um elétron encontra-se num poço de potencial unidimensional com barreiras infinitas, situado entre . No instante , a função de onda deste elétron é dada por , sendo uma constante real.

Encontre a derivada na posição no instante . Expresse sua resposta em termos de e das constantes universais.

Justique se o estado acima é estacionário.

Seja uma partícula de massa confinada em uma região entre e no eixo .

a) Por substituição direta na equação de Schrodinger, mostre que a função de onda é uma solução possível para o estado dessa partícula e encontre o valor de sua energia.

b) A função de onda também é solução? Explique.

c) Se é sabido que a partícula se encontra em seu quinto estado de energia, esboce, em função de , a probabilidade de encontrar a partícula em uma posição qualquer.

d) Seja o caso dessa partícula ser o elétron e . Qual é o comprimento de onda do fóton emitido quando o elétron salta do quinto para o primeiro nível de energia?

a) Ao incidir luz sobre um determinado metal, elétrons são arrancados de sua superfície com uma energia cinética máxima igual ao dobro de sua função trabalho. Sabendo que a frequência de corte para esse metal é , qual é o comprimento de onda da luz incidente?

b) Um átomo de Hidrogênio em seu estado de energia mais baixo absorver um fóton com comprimento de onda igual a . Qual é o raio da órbita do elétron no estado final?

c) Um elétron, confinado em um poço de potencial infinito entre as posições e , tem energia igual a . Escreva a função de onda associada a esse elétron.

Uma partícula de massa encontra-se confinada em uma caixa unidimensional , descrita pela região . A energia potencial é para pontos no interior da caixa e para pontos fora da caixa. As equações do formulário podem ser usadas sem demonstração. NÃO substitua os valores das constantes fundamentais na resposta final de cada item.

a) Determine a energia do segundo estado excitado do sistema.

b) Determine a função de onda independente do tempo (normalizada) do estado fundamental.

Uma partícula de massa encontra-se confinada em uma caixa unidimensional , descrita pela região .

A energia potencial é para pontos no interior da caixa e para pontos fora da caixa.

1. Obtenha a expressão geral para os níveis quânticos de energia.
2. Encontre as funções de onda normalizadas associadas a estes níveis.
3. Ao diminuir-se o valor de , o que ocorre com a energia do estado fundamental? Discuta este fato de maneira breve, em termos puramente qualitativos.
4. Qual é a probabilidade de se encontrar a partícula na região para o estado excitado do sistema?

As funções de onda correspondentes aos estados estacionários de uma partícula de massa que se move em uma dimensão confinada em um poço de potencial infinito de largura são dadas por

Determine a expressão para o comprimento de onda de de Broglie desta partícula para o estado correspondente a

Estime a incerteza mínima na medida do momento linear desta partícula no estado .

Suponha agora que no instante , a partícula encontra-se em um estado dado pela superposição de dois estados estacionários na forma , onde e representam a parte espacial das soluções estacionárias para e , respectivamente, e uma constante. Obtenha e . Expresse sua resposta em termos de e e das demais grandezas que caracterizam o sistema.

O estado acima é um estado estacionário? Justifique sua resposta.

Um elétron livre se move no sentido positivo do eixo x com velocidade v. Ele obedece a equação de onda de Schrödinger. Essa equação para o citado elétron tem uma função de onda dada por Ψ(𝑥,𝑡) = .

(c) Use o operador do momento linear na função de onda Ψ(𝑥,𝑡) para obter o autovalor (p) do momento linear desse elétron.

Faça a escolha correta e justifique: A energia no estado fundamental de um elétron confinado em uma caixa unidimensional de comprimento 𝐿 = 0,2 𝑛𝑚 é:

(a) 1,88 eV

(b) 4,47 eV

(c) 6,25 eV

(d) 9,38 eV.

Um elétron livre se move no sentido positivo do eixo x com velocidade v. Ele obedece a equação de onda de Schrödinger. Essa equação para o citado elétron tem uma função de onda dada por Ψ(𝑥,𝑡) = .

Uma partícula livre se move no sentido positivo do eixo x com velocidade v. A solução da equação de Schrödinger para esse caso é dada por . Obtenha o valor (p) do momento linear dessa partícula.

Uma partícula não relativística com energia de repouso de está confinada em uma caixa unidimensional de tamanho , ocupando o primeiro estado excitado. Determine o tamanho para que a energia cinética da partícula seja dada por .

a) .

b) .

c) .

d) .

e) .

Encontre a função de onda independente do tempo do primeiro estado excitado para uma partícula confinada em uma caixa unidimensional de largura .

a) Um elétron livre tem energia e se propaga da esquerda para a direita ao longo do eixo . A partir da Eq. De Schrodinger, encontre a função de onda que o representa (a menos de uma constante de normalização) e ache o comprimento de onda de de Broglie associado ao elétron se .

b) Se uma partícula está no quarto nível de energia de um poço infinito de largura , qual é a probabilidade de encontrá-la no primeiro 1/8 do poço?

c) Determinadas partículas são muito instáveis e se desintegram em um tempo muito pequeno. Por causa do Princípio da Incerteza, sua massa de repouso não pode ser determinada exatamente. Uma partícula elementar chamada méson tem massa média de com uma incerteza de massa de . Estime o tempo de vida do méson , em segundos.

Uma partícula de massa está confinada em um tubo de comprimento .

O momento linear e a energia dessa partícula são respectivamente iguais a:

Considere o movimento unidimensional de uma partícula de massa m sujeita a um potencial que é nulo na região e infinito para ou

(a) Escreva a função de onda nas regiões e . Justifique sua resposta.

(b) Escreva a equação de Schrödinger para a região e utilizando as condições de contorno, obtenha a expressão para a função de onda normalizada

(c) Determine os possíveis valores dos níveis de energia em termos dos parâmetros do enunciado e de

Considere um elétron que esteja confinado dentro de um poço de potencial unidimensional, com altura infinita e largura d.

(a) Escreva a equação de Schrödinger independente do tempo para este elétron na região (dentro do poço).

(b) Obtenha as soluções normalizadas do problema acima e as correspondentes energias permitidas para o elétron na região

(c) Considere agora que o elétron se encontra no estado quântico descrito pela função de onda , sendo A a constante de normalização obtida no item (b). Determine o comprimento de onda de de Broglie e o momento linear associado à este estado.

(d) Para o mesmo estado do item (c), determine a probabilidade de encontrar o elétron entre e

.

Seja um elétron confinado em um poço infinito de largura , sendo sua função de onda correspondente ao segundo estado de energia. Calcule a probabilidade de encontrar o elétron em uma janela de em torno do ponto médio do poço.

Uma partícula se encontra dentro de uma caixa unidimensional de tamanho e possui energia . Determine o estado estacionário ocupado pela partícula.

a) Estado fundamental.

b) Primeiro estado excitado.

c) Segundo estado excitado.

d) Terceiro estado excitado.

e) Quarto estado excitado.