Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 12
Um engradado de massa de 10,0 kg é puxado por uma inclinação áspera com velocidade escalar inicial de 1,50 m/s. A força para puxar o engradado é 100 N paralela com a inclinação, formando um ângulo de 20,0° com a horizontal. O coeficiente de atrito cinético é 0,400 e o engradado é puxado por 5,00 m. (a) Quanto trabalho é realizado pela força gravitacional no engradado? (b) Determine o aumento em energia interna do sistema engradado-inclinação por causa do atrito. (c) Quanto trabalho é realizado pela força de 100 N no engradado? (d) Qual é a variação na energia cinética do engradado? (e) Qual é a velocidade do engradado depois de ser puxado por 5,00 m?
Passo 1
(a)A formulinha pro trabalho da força gravitacional, a gente já sabe, tem essa formulinha:
Aqui a gente conhece e a gente pode considerar . Mas a gente não sabe ainda, só que a gente tem como descobrir a partir do seguinte esqueminha, que representa o deslocamento de 5 metros do engradado pela inclinação:
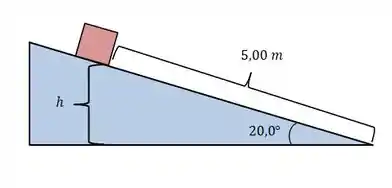
Agora encontrar é tranquilo, gente, fazemos isso por trigonometria! Você sabe que , então vamos aplicar isso pra , que vale .
Com isso, a gente tem:
Por fim, a gente calcula o trabalho da força gravitacional:
Passo 2
(b)Pra isso a gente precisa calcular o trabalho da força de atrito!
A formulinha a gente conhece, que é essa:
Onde é o deslocamento do engradado, que vale e tem a seguinte formulinha:
Sendo o coeficiente de atrito, que vale e é a força normal. A força normal a gente não tem, e então precisamos determinar seu valor a partir do esqueminha do Passo 1.
Vamos fazer o diagrama de corpo livre no engradado, e assim a gente vai descobrir o valor pra . Observa bem:
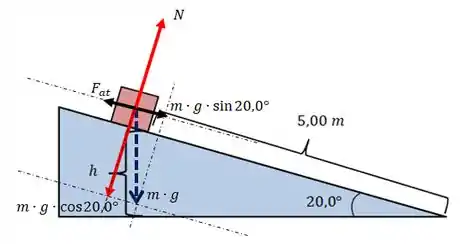
Como o engradado não flutua e nem afunda na rampa que ele sobe, naturalmente as forças e (decomposição da força peso, , a direção normal) precisam ser iguais!
Com isso, a gente escreve:
Agora só aplicar os dados que a gente já tem e determinamos ! A gente vai ter:
Maravilha, amores, agora a gente consegue calcular o trabalho da força de atrito! Só aplicar na primeira equação os dados que a gente já tem, e daí vamos determinar!
A gente vai ter:
Passo 3
(c)O trabalho dessa força, como pra qualquer outra, vai ter a formulinha:
Sendo e , a gente tem:
Passo 4
(d)Pela lei da conservação de energia, a gente tem:
Ou seja, a energia total do sistema (energia mecânica) é a soma das energias cinética e potencial. A gente pode colocar deltas em cada um desses termos, indicando a variação de cada uma. Olha só, você vai entender:
Bom, o valor pra variação da energia mecânica vai ser o somatório entre o trabalho da força potencial gravitacional , a força , menos o trabalho da força de atrito, que “remove” energia do sistema.
Nisso, a gente tem:
A variação da energia potencial gravitacional vai valer, como a gente já calculou:
Com isso, a gente consegue determinar :
Passo 5
(e)A gente calcula a velocidade final a partir da variação da energia cinética que a gente acabou de calcular. A gente tem o seguinte:
Resposta
(a)
(b)
(c)
(d)
(e)