Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 67

Uma certa mola não obedece à lei de Hooke; ao ser comprimida ou esticada, ela exerce uma força restauradora com módulo F x x = - α x - β x 2 , onde α = 60,0   N / m e β = 18,0   N / m 2 . A massa da mola é desprezível. a) Calcule a função energia potencial U ( x ) dessa mola. Considere U = 0 para x = 0 . b) Um objeto de massa igual a 0,900 kg apoiado em uma superfície horizontal sem atrito está preso a essa mola, sendo puxado para a direita (no sentido + x ), esticando a mola até uma distância de 1,0 m, e a seguir é libertado. Qual é a velocidade do objeto no ponto situado a 0,50 m à direita do ponto de equilíbrio x = 0 ?

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos uma situação onde a Lei de Hook não é obedecia, temos uma deformação que não segue linearmente a força que é aplicada.

Iremos utilizar da relação W = - ∆ U

Para nos ajudar a resolver essa atividade.

Passo 2

  1. Fala aí! Tudo bom? Para resolver esse problema vamos separando as informações do enunciado, organizando a ideia que saíremos no resultado.

    2. Temos que:

    F x x = - α x - β x 2

    Com:

    α = 60,0   N / m   β = 18,0   N / m 2

    E ele pede para achar a função U x dessa mola com essas informações. Agora a gente vai precisar pensar em umas expressões para nos ajudar. Bora lá!

    Se tivermos dois pontos (1) e (2) para analisar a variação de energia potencial. Vamos lembrar que

    W = - ∆ U

    W trabalho

    Δ U diferença da energia potencial

    Então:

    W = U 1 - U 2

    Mas a gente pode lembrar também que o trabalho W entre x 1 e x 2 é a integral da força que causa o trabalho entre essas duas posições:

    W = ∫ x 1 x 2 F x d x

    Substituindo

    ∫ x 1 x 2 F x ( x ) d x = U 1 - U 2

    Ele nos diz que x 1 = 0 e U 1 = 0 . E podemos fazer x 2 como algum seja algum ponto arbitrário.

    ∫ 0 x 2 F x ( x ) d x = - U 2

    Substituindo a força que o enunciado deu:

    U 2 = - ∫ 0 x 2 - α x - β x 2 d x

    Passo 3

    Vamos calcular essa integral:

    U 2 = - ∫ 0 x 2 - α x - β x 2 d x

    U 2 = ∫ 0 x 2 α x + β x 2 d x

    Substituindo o valor das constantes:

    U 2 = ∫ 0 x 2 60 x + 18 x 2 d x

    Usando a regrinha de integrar polinômios:

    U 2 = 60 x 2 2 + 18 x 3 3 0 x 2 = 30 x 2 2 + 6 x 2 3

    Achamos uma função que descreve a energia potencial de F x em um ponto arbitrário x 2 .

    Se a gente só mudar a variável dessa função de x 2 que achamos por x , olha o que achamos:

    U x = 30 x 2 + 6 x 3

    A função potencial de F x em um ponto arbitrário x como ele pede. 😉

    Passo 4

  2. Nesse caso, para achar a velocidade do objeto, vamos começar aplicando a equação da lei da conservação da energia.

Vamos esboçar o sistema do ponto 1 e do ponto 2:

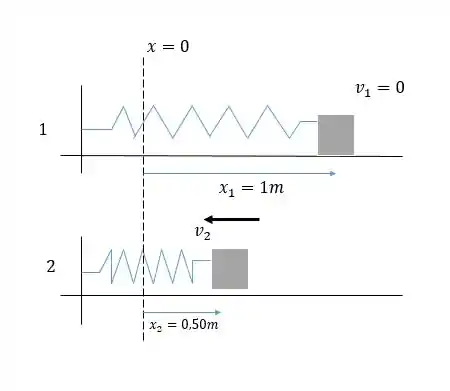
Temos que:

K 1 + U 1 + W e x t = K 2 + U 2

E como, a única força que funciona no objeto é a força da mola, o trabalho causado por uma força externa é:

W e x t = 0

Assim:

K 1 + U 1 = K 2 + U 2

Passo 3

Temos que:

K 1 = 0 K 2 = 1 2 m v 2 2

Já que em 1 o objeto está parado e em 2 o objeto está se movendo. Achando a energia potencial em cada ponto pela expressão que encontramos

U 1 = U x 1 = 30 x 1 2 + 6 x 1 3

= 30 ⋅ 1 2 + 6 ⋅ 1 3

= 36 J    

E

U 2 = U x 2 = 30 x 2 2 + 6 x 2 3

= 30 ⋅ 0,500 2 + 6 ⋅ 0,500 3

= 8,25 J  

Então, a equação da conservação fica

K 1 + U 1 = K 2 + U 2

0 + 36 = 1 2 m v 2 2 + 8,25

Isso implica que:

v 2 = 2 ⋅ ( 36 - 8,25 ) 0,900 = 7,85 m / s

A energia potencial elástica armazenada na mola diminui e a energia cinética do objeto aumenta.

Resposta

  1. U x = 30 x 2 + 6 x 3 .
  2. v 2 = 7,85 m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que, quando os freios são aplicados, uma força de atrito constante é exercida pela estrada sobre as rodas de um carro. Neste caso, quais das seguintes afirmativas são necessariamente verdadeir
Uma embarcação esportiva de 285k g é dirigida, na superfície de um lago, com a rapidez constante de 13,5m / s , de encontro a uma rampa inclinada de 25,0 ° acima da horizontal. O coeficiente de atrito
Uma tradicional experiência de laboratório de física básica, que trata da conservação de energia e das leis de Newton, é mostrada na Figura 7-57. Um carrinho deslizante é colocado sobre um trilho de a
Um reboque para esquiadores está sendo desenhado, para uma nova área de prática de esqui. Ele deve ser capaz de puxar um máximo de 80 esquiadores em uma subida de 600m , inclinada de 15 ° acima da hor
Um bloco de massa m desliza com rapidez constante por um plano inclinado a um ângulo θ com a horizontal. Deduza uma expressão para a energia dissipada pelo atrito em um invervalo de tempo Δ t .