Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 65

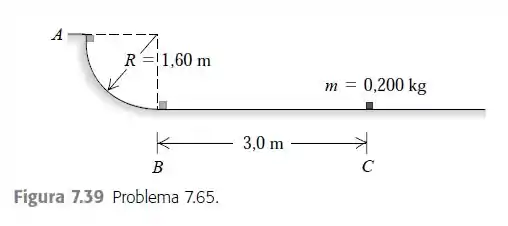
Em um posto para carga de caminhões do correio, um pacote de 0,200   k g é largado do repouso no ponto A sobre um trilho com forma de um quarto de circunferência de raio igual a 1,60   m (Figura 7.39). O tamanho do pacote é muito menor do que 1,60   m , de modo que ele pode ser considerado como uma partícula. Ele desliza para baixo ao longo do trilho e atinge o ponto B com uma velocidade de 4,80   m / s . Depois de passar pelo ponto B, ele desliza uma distância de 3,0   m sobre uma superfície horizontal até parar no ponto C. a) Qual é o coeficiente de atrito cinético entre o pacote e a superfície horizontal? b) Qual é o trabalho realizado pela força de atrito ao longo do arco circular do ponto A ao ponto B?

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Então é o seguinte, nessa situação temos a inicialmente um corpo com energia potencial gravitacional, essa energia é convertida em energia cinética porém também temos a perda de energia por conta do trabalho da força de atrito.

Sei que parece muita coisa, mas vamos dividir e equacionar tudo direitinho e você vai entender.

Passo 2

  1. Oi, galerinha! Tudo bom? O pacote parte do repouso e vai ganhando velocidade ao longo da descida, onde ele encontra um plano horizontal e desliza até parar. A gente consegue resolver esses problemas aplica a lei de conservação da energia!

    2. Vamos a conservação de energia ao movimento de B para C:

    E B = E C

    K B + U B + W o u t r a = K C + U C

    K energia cinética

    U energia potencial gravitacional

    W trabalho de outras forças

    Tomando a superfície horizontal como referência, temos que no ponto B e C , a altura será zero, ou seja, sua energia potência será zero.

    K B + 0 + W o u t r a = K C + 0

    Como o bloco desliza até o repouso, temos que a energia cinética de C também será zero, ou seja,

    K B + 0 + W o u t r a = 0

    Passo 3

    A única força que funciona na embalagem durante essa parte do movimento é o atrito, então,

    W o u t r a = W f = f k ( cos ⁡ ϕ ) s = μ k m g   ( cos ⁡ 180 ° ) s = - μ k m g s

    ϕ = 180 º pois a força de atrito se opõe ao movimento do corpo.

    Como,

    K B = 1 2 m v B 2

    Então,

    K B + W f = 0

    1 2 m v B 2 - μ + k   m g s = 0

    E

    μ k = μ s 2 2 g s = ( 4,8 ) 2 2 ⋅ 9,8 ⋅ 3 = 0,392

    Passo 4

  2. Agora, vamos aplicar a conservação de energia ao movimento de A para B:

K A + U A + W o u t r a = K B + U B

O trabalho é feito pela gravidade e pelo atrito, então,

W o u t r a = W f

Como,

K A = 0

E

K B = 1 2 m v B 2 = 1 2 ⋅ 0,200 ⋅ ( 4,8 ) 2 = 2,304 J

E

U A = m g y A = m g R = 0,200 ⋅ 9,8 ⋅ 1,60 = 3,136 J

E

U B = 0

Então,

U A + W f = K B

Isso implica que:

W f = K B - U A = 2,304 J - 3,136 J = - 0,83 J

Resposta

  1. 0,392
  2. - 0,83 J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em 1964, depois que o automóvel a jato Spirit of America, de 1250k g , perdeu seu pára-quedas e se desecontrolou em uma corrida em Bonneville Salt Flats, no Utah (EUA), foram deixadas marcas de derrap
Uma caixa de massa m , sobre o chão, está conecetada a uma mola horizontal de constante de força k (veja a figura). O coeficiente de atrito cinético entre a caixa e o chão é μ k . A outra ponta da mol
(a) Calcule a energia cinética de um carro de 1200k g que se move a 50k m / h . (b) Se o atrito (de rolamento e de arraste do ar) resulta em uma força retardadora de 300N a uma rapidez de 50k m / h ,
Um carrinho desliza do alto de uma montanha russa de 5 m de altura, com atrito desprezível. Chegando ao ponto A , no sopé da montanha, ele é freiado pelo terreno A B coberto de areia, parando em 1,25
Um bloco de massa m=5 Kg, deslizando sobre uma mesa horizontal com coeficientes de atrito cinético e estático 0,5 e 0,6 , respectivamente, colide com uma mola de massa desprezível, de constante de mol