Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 41
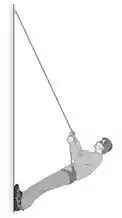
Escaladores de montanhas geralmente usam uma corda para descerem pela encosta de um penhasco (essa manobra é denominada rapel). Eles descem pela encosta com o corpo praticamente horizontal e os pés apoiados contra o penhasco (Figura ). Suponha que um escalador de e de altura, com o centro de gravidade localizado a dos pés, desça fazendo rapel por uma encosta vertical com o corpo erguido a acima do plano horizontal. Ele segura a corda a dos pés, e ela forma um ângulo de com a face da encosta. a) Qual tensão essa corda deve suportar? b) Ache os componentes horizontal e vertical da força que a face da encosta exerce sobre os pés do escalador. c) Qual é o coeficiente de atrito mínimo para impedir que os pés do escalar escorreguem pela face da encosta, se ele apoiar um
pé de cada vez contra a encosta?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular (a) a tensão que a corda deve suportar, (b) as componentes horizontal e vertical da força que a encosta exerce sobre os pés do escalador e (c) o coeficiente de atrito mínimo para impedir que ele escorregue.
Pra isso, vamos construir um diagrama de corpo livre do nosso sistema e usar a equação do equilíbrio de torques para obter o valor da tensão na corda, que vai ser igual a força peso naquela direção. Depois, vamos usar as equações do equilíbrio de forças, e , para obter as componentes da força que a encosta exerce sobre o escalador. E por fim, vamos calcular o coeficiente mínimo de atrito , usando a fórmula:
Onde, nesse caso, representa a componente vertical da força exercida pela encosta e a sua componente horizontal.
Vamos lá!
Passo 2
Vamos começar esboçando um diagrama de corpo livre para o alpinista:
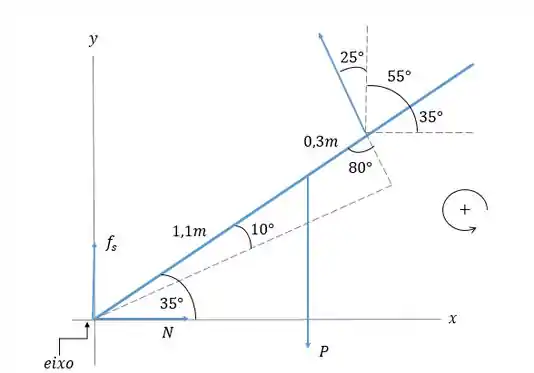
Repare que e são as componentes vertical e a horizontal da força exercida pela face do penhasco no alpinista. O braço do momento para a força é
a) Então, aplicando , temos que:
Sabendo que representa a tensão na corda, essa equações nos dá:
Passo 3
b) Agora fazendo o somatório de forças horizontais no nosso sistema, através da equação de equilíbrio , temos que:
Que é a nossa componente horizontal da força exercida pela encosta no alpinista.
Da mesma forma, para as forças verticais, temos , que nos dá:
E então, a componente vertical da força da encosta será:
Passo 4
c) Por fim, para calcularmos o coeficiente de atrito mínimo , vamos ter:
Então, substituindo os valores obtidos no passo anterior, temos:
Para atingir esse grande valor de o alpinista deve usar sapatos especiais de sola áspera.
Valeu, galera! Até a próxima! 😉