Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 67
Dois amigos transportam uma caixa de subindo os degraus de uma escada. A caixa possui de comprimento e altura de , com centro de gravidade localizado em seu centro. Os degraus da escada possuem uma inclinação de com a horizontal, de modo que sua aresta inferior é paralela à inclinação da escada (Figura 11.51). Supondo que a força aplicada pelos amigos sobre a caixa possua direção vertical, qual é o módulo de cada uma dessas forças? Quem realiza mais esforço, o que está na parte de cima ou aquele que está na parte de baixo da escada?
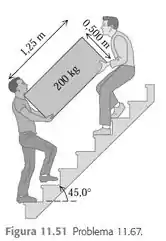
Passo 1
Faaala galeraa, bora fazer mais uma questão?
O enunciado pediu pra gente encontrar o módulo de cada uma dessas forças e quem realiza mais esforço no transporte dessa caixa.
Para resolver essa questão, vamos aplicar a primeira e a segunda condições de equilíbrio para a caixa.
Mas para a gente não se esquecer de nenhuma forma, vamos desenhando seu diagrama de corpo livre, temos:
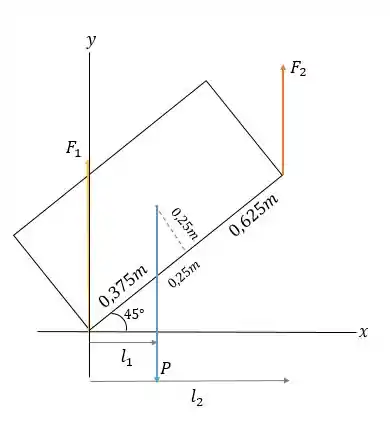
Onde e são as forças verticais exercidas por você e seu amigo. Tome como a origem no canto inferior esquerdo da caixa.
Organizando o que vamos fazer: primeiro vamos descobrir a força total aplicada para depois descobrir a força em cada ponto da caixa.
Agora vamos aplicar!
Passo 2
a) Feito essa analise, vamos aplicar a primeira condição de equilibrio:
Essa é força total aplicada, agora vamos descobrir o modulo de cada uma das forças!
Passo 3
Usando a condição
Temos que:
Substituindo os dados do enunciado:
E então calculando a outra força:
Substituindo os valores:
Logo, a pessoa abaixo (você) aplica uma força de . A pessoa acima (seu amigo) aplica uma força de
Valeu, galera! Até a próxima! 😉