Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.Problemas - Ex. 42
Sir Lancelot cavalga lentamente para fora do castelo em Camelot atravessando a ponte levadiça de de comprimento que passa sobre o fosso (Figura ). Ele não sabe que seus inimigos enfraqueceram parcialmente o cabo que sustenta a extremidade frontal da ponte, de modo que ele deve romper sob uma tensão de . A ponte possui massa igual a e seu centro de gravidade está localizado em seu centro. Lancelot, sua lança, sua armadura e seu cavalo possuem massa igual a . Verifique se o cabo se romperá antes que Lancelot atinja a extremidade da ponte. Caso ele se rompa, qual é a distância entre o centro de gravidade do cavalo e do cavaleiro no momento em que o cabo se rompe?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente verificar se o cabo vai se romper antes de Lancelot atingir a extremidade da ponte e, se o cabo de romper, determinar a distância distância entre o centro de gravidade do cavalo e do cavaleiro no momento em que o cabo se rompe.
Cara, provavelmente teve algum erro na hora de traduzir a questão para português, na verdade a questão quer, caso o cabo se rompa, a distância máxima que Lancelot pode chegar em relação ao início da ponte, ok??
Vamos ver qual o DCL na ponte:
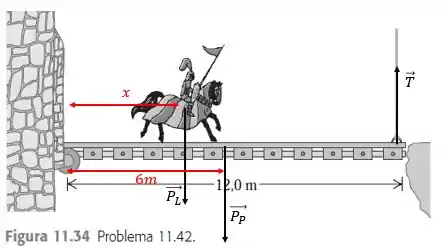
Onde é a tensão no cabo, é o peso da ponte e é o peso do Lancelot com o cavalo e todo o aparato dele. Além disso, é a distância do Lancelot para o início da ponte.
Nós vamos aplicar o equilíbrio de torque na ponte:
Onde o eixo de rotação estará na extremidade esquerda da ponte e os torques no sentido anti-horário serão positivos, ok?
Então, como , repare que quanto maior a distância da força para o eixo de rotação, maior o torque, certo?? Então, vamos pegar a situação mais extrema do Lancelot em relação à ponte: quando ele está no final dela (), pois aí seu torque será o maior possível em relação ao nosso eixo de rotação. E, com isso, vamos achar o valor da tensão no cabo e ver se é maior ou não que a tensão máxima suportada .
Assim, vamos ver se é possível o sistema estar em equilíbrio sem o cabo se romper!
Passo 2
Se Lancelot estivesse no final da ponte, a equação de equilíbrio dos torques ficaria:
Isolando :
Como os pesos podem ser calculados por :
Substituindo os valores:
Então:
Isso excede a tensão máxima que o cabo pode ter, então isso faz com que o cabo se rompa!
Passo 3
Agora, para encontrar a distância máxima que Lancelot pode percorrer sem romper o cabo, substituiremos o por e vamos descobrir o valor de , que é a distância máxima do Lancelot para o início da ponte. Mas vamos continuar usando o equilíbrio de torques do passo anterior:
Isolando :
Então:
Substituindo os valores que temos:
Então, Lancelot pode chegar a de distância do início da ponte sem que o cabo se rompa.
Valeu, galera! Até a próxima! 😉