Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 88
Uma esfera maciça e uniforme rola descendo um plano inclinado, sem deslizar. Se a aceleração linear do centro de massa da esfera é , qual é o ângulo de inclinação do plano com a horizontal?
Passo 1
Se liga, galerinha! Se a esfera está rodando, tem que ter uma força no ponto de contato da esfera com o plano que atue de forma a fazê-la rodar. Qual é a única força possível para isso? A força de atrito! O diagrama de forças da situação tá feito aqui:
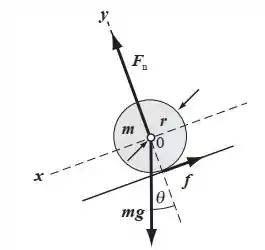
Passo 2
Olhando para a rotação da esfera:
Mas a gente sabe que , e conhecemos o momento de inércia de uma esfera maciça!
Para o movimento de descida da esfera, vamos aplicar a segunda lei de Newton:
Cortando a massa e dando uma ajeitada:
Passo 3
Agora é só substituir os valores numéricos:
Resposta
Exercícios de Livros Relacionados
Um disco sólido rola sem deslizar sobre uma superfície horizontal com velocidade constante de 2,50 m/s. a) Se o disco rola para cima de uma rampa inclinada a 30,0º, qual é a distância máxima que ele a
O ioiô. Um ioiô é feito usando-se dois discos uniformes, cada um com massa m e raio R ligados por um eixo leve de raio b. Um fio leve e fino é enrolado diversas vezes em torno do eixo e a seguir manti
Uma bola de gude homogênea rola sem deslizar para baixo da trajetória indicada na Figura 10.59, partindo do repouso. a) Ache a altura mínima h necessária para que a bola de gude não caia na cova.b) O
Uma criança faz uma bola de basquete de 0,600 kg rolar para cima de uma rampa longa. A bola de basquete pode ser considerada uma casca esférica, de paredes finas. Quando a criança larga a bola na base
Uma bola maciça e uniforme rola sem deslizar para cima de uma colina, como indica a Figura 10.61. No topo da colina, ela se move horizontalmente e cai pelo rochedo vertical. a) A que distância da base