Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 76
Uma bola maciça e uniforme rola sem deslizar para cima de uma colina, como indica a Figura 10.61. No topo da colina, ela se move horizontalmente e cai pelo rochedo vertical.
a) A que distância da base do rochedo a bola aterrissa e com que velocidade ela está se movendo assim que cai?
b) Note que, quando a bola aterrissa, ela possui uma velocidade escalar de translação maior do que quando estava na base da colina. Isso significa que de alguma forma a bola ganhou energia? Explique!
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma bola maciça e uniforme rola sem deslizar para cima de uma colina, como indica a figura abaixo.
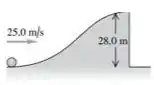
No topo da colina, ela se move horizontalmente e cai pelo rochedo vertical.
Queremos calcular a distância da base do rochedo onde a bola aterrissa e com que velocidade ela está se movendo assim que cai.
Para isso, devemos usar o princípio de conservação da energia:
Onde é a nergia potencial e é a energia cinética (os termos com significa que estão no instante inicial e com , o instante final).
O enunciado também nos diz que quando a bola aterrissa, ela possui uma velocidade escalar de translação maior do que quando estava na base da colina.
Queremos saber se isso significa que de alguma forma a bola ganhou energia.
Bora lá!! 😉
Passo 2
Pela conservação de energia, temos:
Onde é a massa do corpo, é a aceleração da gravidade, é a altura, é a velocidade, é o momento de inércia e é a velocidade angular.
Como . Então,
Logo,
Passo 3
Agora, consideramos o movimento vertical. Como , substituiremos em
Na horizontal, temos
Analisando, então, a velocidade
Logo,
Passo 4
Quando a bola aterrissa, ela possui uma velocidade escalar de translação maior do que quando estava na base da colina.
Isso se deve ao fato de que a energia cinética total é a mesma. No entanto, a energia cinética translacional aumentou e a rotacional diminuiu.
Resposta
a) e ;
b) a energia cinética translacional aumentou e a rotacional diminuiu.