Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.Problemas Adicionais - Ex. 77
Uma esfera não condutora tem uma densidade volumétrica de cargas uniforme . Seja r o vetor que liga o centro da esfera a um ponto genérico P no interior da esfera. (a) Mostre que o campo elétrico no ponto P é dado por . (Observe que o resultado não depende do raio da esfera.) (b) Uma cavidade esférica é aberta na esfera, como mostra a Fig. 23-56. Usando o princípio da super posição, mostre que o campo elétrico no interior da cavidade é uniforme e é dado por , onde é o vetor que liga o centro da esfera ao centro da cavidade.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
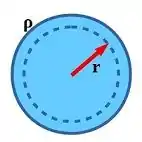
Aqui temos uma esfera não condutora com uma densidade volumétrica dada, a imagem abaixo nos ajuda um pouco a ver como a situação.
A esfera não condutora com densidade de carga uniforme é mostrado abaixo. Para encontrar o campo elétrico em um ponto dentro da esfera cujo vetor de posição é , podemos fazer uso da lei de Gauss.
Passo 2
(a) Para calcular o módulo do campo elétrico dentro da esfera, vamos utilizar a lei de Gauss:
Primeiramente vamos encontrar a carga envolvida, :
Onde V é o volume da superfície Gaussiana, nesse caso vamos escolher uma casca esférica de raio r menor que a esfera não condutora. Portanto:
e
Como, nessa superfície o módulo do campo é constante:
Como o campo tem direção radial:
Passo 3
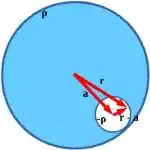
(b) Podemos imaginar que essa cavidade é na verdade uma esfera de densidade volumétrica de carga , dentro da esfera maior de carga . Portanto, para calcular o campo gerado por essas duas esferas, basta somar o campo gerado individualmente por cada uma:
Resposta
(a)(b)