Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 44
Uma esfera de raio em densidade volumétrica de carga para onde é uma constante e para . (a) Determine a carga total na esfera. (b) Determine as expressões para o campo elétrico no interior e no exterior da distribuição de cargas. (c) Represente a magnitude do campo elétrico como uma função da distância ao centro da esfera.
Passo 1
Fala ai gente. Vocês repararam que os três últimos exercícios são praticamente iguais, mudando apenas a função ? Vamos então aplicar a ideia que usamos nos dois últimos exercícios.
Passo 2
- Temos que
- Para pontos internos, temos . Assim,
- Veja o gráfico a seguir:
Passo 3
Para pontos externos, temos . Assim,
Passo 4
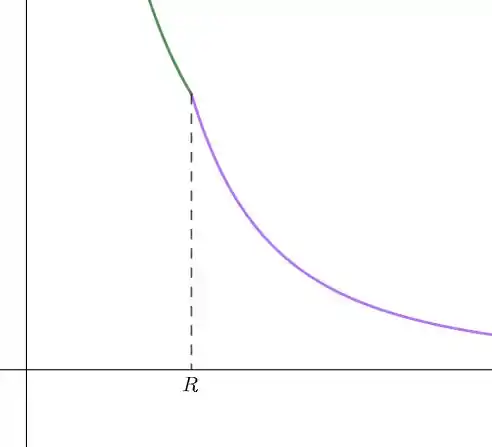
Note, mais uma vez, que o campo elétrico é contínuo em matérias isolantes.
Resposta
- e
- Ver gráfico acima.
Exercícios de Livros Relacionados
A Eq. 25-12 E = σ ϵ 0 nos dá o campo elétrico para pontos próximos de uma superfície condutora carregada. Aplique-a a uma esfera condutora de raio r e carga q , e mostre que o campo elétrico fora da e
Um próton descreve um movimento circular com velocidade escalar v = 3,00 × 10 5 m / s ao redor e imediatamente fora de uma esfera carregada, de raio r = 1,00c m . Qual é a carga sobre a esfera.
Uma esfera maciça, não condutora, de raio R , tem uma distribuição de carga não uniforme de densidade volumétrica dada por ρ = ρ 1 r R , onde ρ 1 é uma constante e r é a distancia ao centro da esfera.
A Fig. 25-40 mostra uma carga puntiforme q = 1,0 × 10 - 7C , no centro de uma cavidade esférica de raio 3,0c m existente numa peça de metal. Use a lei de Gauss para determinar o campo elétrico (a) no
Uma casca esférica, fina e descarregada, tem uma carga puntiforme q no centro. Deduza expressões para o campo elétrico (a) no interior da casca e (b) fora da casca, usando a lei de Gauss. (c) A casca