Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 83

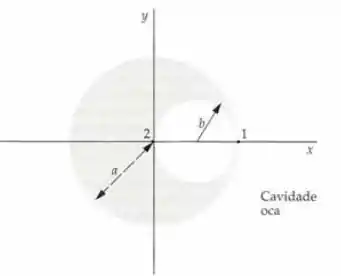
Uma esfera sólida não condutora e uniformemente carregada, com raio R , tem seu centro na origem e tem uma densidade volumétrica de carga ρ . (a) Mostre que em um ponto no interior da esfera a uma distância r do centro E → = ρ 3 ε 0 r r ^ . (b) É removido material da esfera formando uma cavidade esférica que tem um raio b = R / 2 e seu centro em x = b no eixo x . (Figura 22-46). Calcule o campo elétrico nos pontos 1 e 2 mostrados na Figura 22-46. Dica: Considere a esfera com a cavidade como duas esferas uniformes com densidades de carga iguais, com sinais contrários.

Passo 1

  1. Podemos aplicar a lei de Gauss. Tomando uma superfície gaussiana, concêntrica com a esfera, de raio r < a , temos que

    2. ∮ E   d A = q i n t ε 0

    A carga interna pode ser calculada por:

    q i n t = ρ V g a u s s i a n a q i n t = ρ 4 3 π a 3

    Logo,

    E 4 π r 2 = 4 3 ρ π a 3 ε 0

    de modo que

    E = ρ r 3 ε 0

    Notemos que E → está na mesma direção que r . Assim, podemos escrever

    E → = ρ r 3 ε 0 r ^

    Passo 2

  2. Vamos utilizar o princípio da superposição:

E → = E → 1 + E → 2

onde

  • E → é o campo elétrico, no ponto 1 , da esfera completa (sem buraco)
  • E → 1 é o campo elétrico da esfera de raio b que foi retirada.
  • E → 2 é o campo elétrico da esfera com o buraco (é o que queremos calcular)

Os valores de E → e E → 1 são fáceis de se calcular usando a fórmula obtida no item (a):

E = ρ r 3 ε 0 = ρ a 3 ε 0

Também, temos que

E 1 = ρ r 3 ε 0 = ρ b 3 ε 0 = ρ ( a / 2 ) 3 ε 0

Logo,

E = E 1 + E 2 ρ a 3 ε 0 = ρ a / 2 3 ε 0 + E 2 E 2 = ρ a 6 ε 0

Notemos que a direção desse campo é no eixo x . Assim,

E → 2 = ρ a 6 ε 0 i ^

Resposta

O campo elétrico é dado por E → 2 = ρ a 6 ε 0 i ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 23-48 mostra o módulo do campo elétrico do lado de dentro e do lado de fora de uma esfera com uma distribuição uniforme de cargas positivas em função da distância do centro da esfera. A escala
Uma carga pontual produz um fluxo elétrico de -750N· m 2 / C através de uma superfície esférica gaussiana de 10,0c m de raio com centro na carga. (a) Se o raio da superfície gaussiana é multiplicado p
A Fig. 23-53 mostra uma casca esférica com uma densidade volumétrica de cargas uniforme ρ=1,84n C / m 3 , raio interno a=10,0c m e raio externo b=2,00 a . Determine o módulo do campo elétrico (a) em r
Duas cascas esféricas concêntricas carregadas têm raios de 10,0c m e15,0c m . A carga da casca menor é 4,00 ×10 - 8C e a da casca maior é 2,00 × 10 - 8C . Determine o campo elétrico (a) em r=12,0c m ;
A Fig. 23-51 mostra duas cascas esféricas não condutoras mantidas fixas no lugar sobre o eixo x . A casca 1 possui uma densidade uniforme de cargas superficiais + 4,0μ C / m 2 na superfície externa e