Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 46
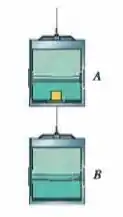
Na Fig.5-44, os elevadores e estão ligados por um cabo e podem ser levantados ou baixados por outro cabo que está acima do elevador . A massa do elevador é ; a massa do elevador é . O piso do elevador sustenta uma caixa de . A tensão do cabo que liga os elevadores é . Qual é o módulo da força normal que o piso do elevador exerce sobre a caixa?
Passo 1
Essa questão é uma aplicação da segunda lei de Newton. Para tanto, é preciso lembrar que a segunda lei de Newton diz:
O problema nos dá a massa dos dois elevadores ( e ), a massa da caixa dentro do elevador (), a tensão do cabo que liga os dois elevadores () e, a partir desses dados, determinar a força normal que o piso do elevador exerce sobre a caixa.
Passo 2
Para iniciar essa questão, vamos analisar o elevador individualmente, sabendo atuam nele duas forças (o peso vertical para baixo e a tração da corda que liga os dois elevadores). Para tanto, vamos escrever a segunda lei de Newton para este caso:
Substituindo os valores conhecidos:
Isolando o :
Passo 3
Sabendo que os elevadores se movem juntos, então a aceleração do conjunto é a mesma. Por isso, vamos aplicar a segunda lei de Newton para a caixa dentro do elevador para determinar a normal, sabendo que só atuam nesta caixa o peso e a força normal de contato entre ela e o elevador. Assim:
Substituindo os valores conhecidos:
Isolando o :