Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 45
Esferas ocas concêntricas. Uma pequena esfera oca condutora, com raio interno e raio externo , é concêntrica com uma grande esfera oca condutora, com raio interno e raio externo (Figura ). A carga total sobre a esfera oca interna é igual a e a carga total sobre a esfera oca externa é igual a . Determine o módulo, a direção e o sentido do campo elétrico em função da distância ao centro comum para as regiões ; ; ; ; . Mostre seus resultados em um gráfico do componente radial de em função da distância . Qual é a carga total sobre a superfície interna da esfera oca pequena; a superfície externa da esfera oca pequena; a superfície interna da esfera oca grande; a superfície externa da esfera oca grande?
Passo 1
Para saber o campo elétrico em cada situação, precisamos considerar uma superfície gaussiana adequada para cada uma delas e lembrar da lei de Gauss dada por:
Agora, vamos dar uma olhada em como ficaria essa configuração dada no enunciado, aonde temos duas esferas ocas concêntricas, cada um com raio interno e externo:
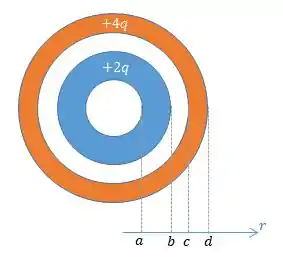
Primeiramente, supondo uma superfície gaussiana esférica de raio , temos que o seu campo elétrico será nulo por não possuir carga em seu interior.
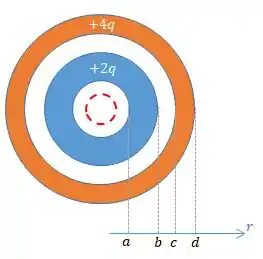
Na região da superfície interna da esfera oca interna, ou seja, em , por se tratar de um condutor carregado, o campo elétrico deve ser nulo. (O campo elétrico dentro de condutores é sempre nulo, beleza?)
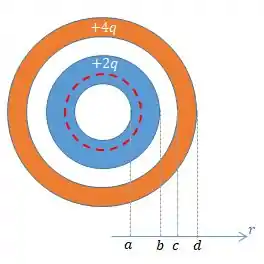
Já para a superfície gaussiana de raio , ela envolve a carga da esfera mais interna com valor .
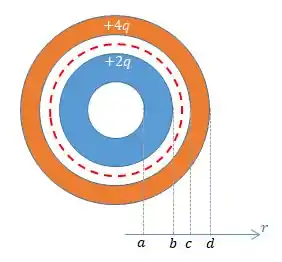
Logo, o seu campo elétrico será dado por:
Já para , por essa ser a região interna da esfera oca maior que é um condutor carregado, seu campo elétrico será nulo.
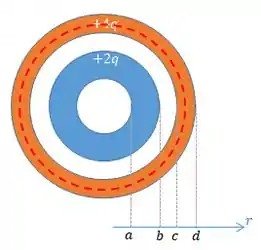
Por fim, tomando a superfície de raio , a carga total envolvida por ela é a soma das cargas sobre a esfera mais interna e a externa.
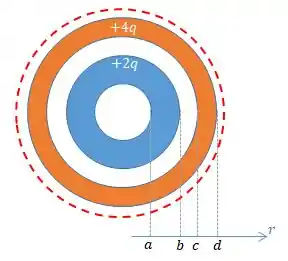
Logo, o campo elétrico é:
Passo 2
O gráfico deste caso pode ser dado por:
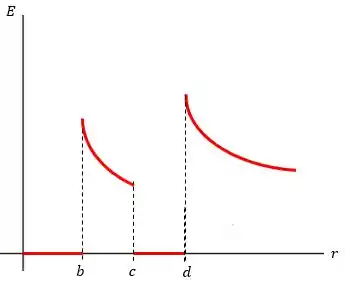
Passo 3
Na região da superfície interna da esfera oca pequena, o campo elétrico deve ser nulo. Por conta disso, o fluxo elétrico também é nulo e, logo, não há carga nessa região.
Agora, para uma superfície gaussiana em , ela envolverá a carga sobre a esfera que tem valor de . Assim, a carga sobre a superfície externa da esfera pequena é .
Da mesma forma, para a superfície interna da esfera oca grande, o campo elétrico em seu interior deve ser nulo. No entanto, como um dos lados dessa esfera oca envolve a carga de da esfera menor, a carga no interior da esfera maior deve ser de mesma intensidade e sinal contrário, ou seja , para que haja “anulação” das cargas e o campo elétrico seja zero.
Para a última região dada por , ambas as cargas sobre as esferas estão envolvidas e, logo, a carga total sobre a superfície externa da esfera oca grande é a soma das cargas que resulta em .