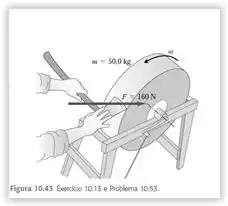
Um esmeril de 50,0 kg é um disco sólido de diâmetro igual a 0,520 m. Você comprime um machado sobre a periferia com uma força normal de 160 N (Figura 10.43). O coeficiente de atrito cinético entre a lâmina e a pedra do esmeril é igual a 0,60, e existe um torque do atrito constante igual a entre o eixo do esmeril e seus mancais.

a) Ache a força que deve ser aplicada tangencialmente à extremidade do eixo da manivela de 0,500 m de comprimento para acelerar a roda do esmeril desde zero até 120 rev/min em 9,0 s. b) Depois que o esmeril atinge a velocidade de 120 rev/min, qual é a força tangencial que deve ser aplicada à extremidade da manivela para manter a velocidade angular constante de 120 rev/min?

c) Quanto tempo o esmeril levaria para reduzir sua velocidade angular de 120 rev/min até zero quando a única força atuante for apenas a força de atrito nos mancais?

Aplicando a fórmula do torque,

Este torque deve ser a soma da força aplicada FR e dos torques de atrito opostos.

Letra b)

Para manter a velocidade angular constante,

Letra c)

Como a única força atuante é a de atrito, utilizaremos somente o torque. Assim, o tempo necessário, será