Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas adicionais - Ex. 102

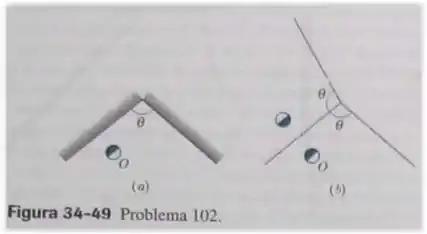
A Fig 34-49 é uma vista de topo de dois espelhos planos verticais com um objeto O entre eles. Quando um observador olha para os espelhos, vê imagens múltiplas do objeto. Para determinar as posições dessas imagens, desenhe o reflexo em cada espelho na região entre os espelhos, como foi feito para o espelho da esquerda na Fig 34-49b. Em seguida, desenhe o reflexo do reflexo. Continue da mesma forma do lado esquerdo e do lado direito até que os reflexos se superponham dos dois lados dos espelhos. Quando isso acontecer, basta contar o número de imagens de O . Determine o número de imagens formadas (a) para θ = 90 ° ; (b) para θ = 45 ° ; (c) θ = 60 ° . Para θ = 120 ° , determine (d) o menor e (e) o maior número de imagens que podem ser observadas, dependendo do ponto de vista do observador e da posição do objeto O . (f) Para cada situação, indique as posições e orientações de todas as imagens de O em um desenho semelhante ao da Fig. 34-49b.

Passo 1

Que questão pesada, mas vamos tentar superá-la.

Passo 2

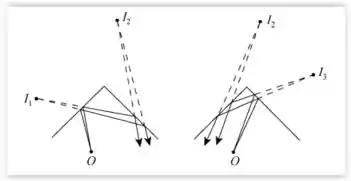
  1. Para θ = 90 , existem três imagens: duas formadas por reflexões em apenas um dos espelhos e a terceira é formada por reflexões sucessivas nos dois espelhos. O diagrama da esquerda mostra a imagem I 1 formada por reflexões do espelho da esquerda. Está à mesma distância do espelho que o objeto O , em uma reta perpendicular ao espelho passando pelo objeto. A Imagem I 2 é formada pela luz refletida nos dois espelhos.

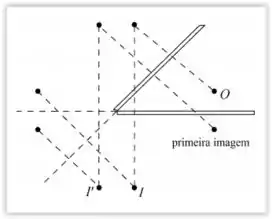
    2. Podemos considerar I 2 como a imagem do prolongamento de I 1 formada pelo espelho da direita. O diagrama da direita mostra a imagem I 3 , formada por reflexões no espelho a direita.

    Passo 3

  2. Para θ = 45 ° , temos duas imagens no segundo espelho, uma causada pelo próprio objeto e outra pela imagem do objeto no primeiro espelho. A partir desses duas imagens, podemos construir duas novas imagens, I e I ' , atrás do primeiro espelho. Prolongando o plano do segundo espelho, podemos encontrar outras dias imagens I e I ' simetricamente disposta em relação ao prolongamento do plano do primeiro espelho. Resumindo, o número de imagens neste caso é 1+2+2+2=7

    3. Passo 4

  3. Para θ = 120 , temos duas imagens, I 1 e I 2 , atrás do segundo espelho e seu prolongamento, causadas pelo objeto e sua primeira imagem (que vamos chamar de I 1 ' ) . Nenhuma outra imagem pode ser construída a partir de I 1 e I 2 , já que as imagens são reflexos mútuos. O número de imagens que podem ser vistas varia de 1 a 3 dependendo da posição do observador e do objeto.

    4. Passo 5

  4. O menor número de imagens que podem ser vista para θ = 120 é 1. Se, por exemplo, o observador está alinhado com o objeto e I 2 , pode ver apenas uma imagem.

    5. Passo 6

  5. O maior número de imagens que podem ser vistas para θ = 120 é 3. Isso acontece quando o observador está razoavelmente afastado dos dois espelhos e aproximadamente equidistante dos espelhos.

    6. Passo 7

  6. Foi feito durante cada item, como solicitado.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Dois espelhos planos fazem um ângulo de 90 ° . A luz de um objeto puntiforme que está posicionado arbitrariamente na frente dos espelhos produz imagens em três posições. Para cada posição da imagem
Mostre que a equação dos espelhos (Equação 32-4 onde f = r / 2 ) fornece a distância imagem correta e a ampliação para um espelho plano.
Quando dois espelhos planos são paralelos, como nas paredes opostas de uma barbearia, surgem imagens múltiplas porque cada imagem em um dos espelhos serve como objeto para o outro espelho. Um objeto e
O furo de uma câmera pinhole fica a uma distância de 12c m do plano do filme, que é um retângulo de 8,0c m de altura por 6,0c m de largura. A que distância de uma pintura de 50c m×50c m deve ser coloc
Um raio luminoso parte do ponto A e chega ao ponto B depois de ser refletido no ponto O, situado na superfície de um espelho. Mostre, sem usar os métodos do cálculo, que a distância AOB é mínima quand