Uma espira quadrada de lado é percorrida por uma corrente .
- Determine, em módulo, direção e sentido, o campo num ponto situado sobre o eixo da espira (reta perpendicular ao seu plano passando pelo centro da espira), à distância de . Para , relacione o resultado com o problema 3.
- Interprete o resultado para .
Passo 1
Se liga! Vamos primeiro visualizar o problema!
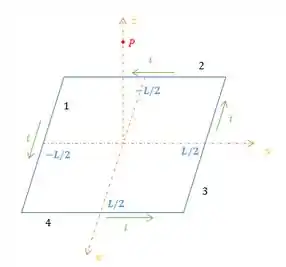
Temos uma espira quadrada de tamanho , onde por ela passa uma corrente como na figura acima. Essa espira é composta por fios de comprimento .
Queremos calcular o campo magnético no ponto que está no eixo da espira, o eixo .
Antes de sair fazendo contas, vale observar o que a simetria do problema nos proporciona.
Pela regra da mão direita, podemos ver que no ponto o fio da esquerda produz um campo que aponta nas direções e e o fio 3 nas direções e . O campo dos dois tem a mesma magnitude, portanto, as componentes se anulam, restando assim apenas a direção .
A mesma coisa ocorrerá com os segmentos 2 e 4. Estes terão campos com componentes (, ) e (, ), respectivamente.
Ou seja, o campo magnético resultante no ponto será na direção .
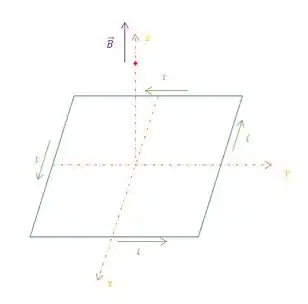
Um macete para se enxergar isso, ao invés de olhar fio por fio, você pode usar a sua mão direita e fechar os seus 4 dedos na direção da circulação da corrente, ao fazer isso, o polegar estará apontando pra cima, indicando que o campo magnético gerado é na direção de .
Passo 2
Já que o campo magnético está na direção de , para calcular o seu módulo iremos calcular as componentes na direção geradas por cada fio e então soma-las.
E pela simetria do problema, como dito anteriormente, essa componente em será a mesma para todos os fios, sendo assim, só precisamos calcular 1 e multiplicar por 4. Vamos calcular então a componente do fio 4 e multiplicá-la por .
(eu escolhi o fio por que ele vai ser mais fácil de calcular, já que ele está apenas no eixo .
Agora precisamos encontrar o campo produzido pelo fio 4.
Precisamos lembrar que o campo devido a um pedaço infinitesimal de um fio é dado por
Onde:
é o vetor infinitesimal que nos dá a direção da corrente que passa no fio, que no caso do fio corre para o sentido positivo de .
é o vetor que nos dá a distância entre um pedaço do fio e o ponto .
Por trigonometria podemos encontrar o módulo desse vetor formando os seguintes triângulos:
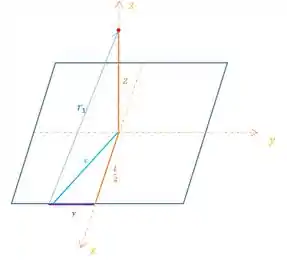
Começando pelo triângulo que está na base da espira, teremos:
E agora usando o triângulo aonde está o vetor :
Sendo assim teremos:
Agora, pra fechar só precisamos encontrar o nosso vetor , que pela figura vemos que ele será:
Agora estamos prontos para prosseguir...
Passo 3
Vimos que um pedaço infinitesimal de campo do fio é dado por:
Pela definição de produto vetorial, vamos calcula-lo através da determinanda da matriz contendo , e as componentes de ambos os vetore:
Agora, para e vem comigo. Lembra que o campo no ponto vai ser apenas a componente no eixo ?
Então, nesse cálculo do campo do fio , eu só preciso me preocupar com a componente do campo que estará na direção de .
Ficaremos então com:
Agora, iremos integrar o campo desse fio, por toda sua extensão, indo de até :
Essa integral tem na tabela. Pela tabela temos
Então, podemos aplicar ao nosso exemplo e então:
Substituindo os limites de integração, teremos:
Passo 4
Agora para encontrar o campo gerado por toda a espira, precisamos multiplicar esse valor por 4!
Passo 5
Para , todas as parcelas que somavam com , teremos que a porção de será muito maior: