Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 62
Uma esquiadora de parte do repouso no topo de uma pista de esqui inclinada com uma altura de .
a) Supondo que as forças de atrito realizem um trabalho total de enquanto ela desce, qual é sua velocidade na base da pista inclinada?
b) Movendo-se agora horizontalmente, a esquiadora atravessa um trecho com neve macia, onde . Sabendo que esse trecho possui extensão de e que a resistência média do ar sobre a esquiadora é igual a , qual é sua velocidade no final desse trecho?
c) A esquiadora colide com um pequeno monte de neve, nele penetrando até parar. Qual é a força média exercida pelo obstáculo até ela parar?
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui a gente tem uma esquiadora descendo de uma rampa, e convertendo a energia potencial gravitacional da altura que ela está em energia cinética. Temos também a ação do atrito que atrapalha o movimento.
A figura abaixo irá te ajudar a visualizar a situação:
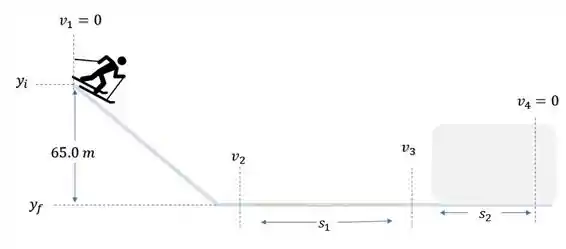
Passo 2
- Por conservação de energia temos:
- Aqui vamos usar a conservação de energia também. A energia cinética inicial vai ser , como encontramos no item anterior. No entanto temos duas formas de dissipação: pelo atrito do chão e pela resistência do ar. Então a energia cinética final dela vai ser igual a energia cinética inicial menos o trabalho realizado pelas dissipações ao longo do percurso:
- Por fim vamos usar o teorema trabalho energia. A energia cinética vai ser zero, uma vez que a esquiadora para. A energia cinética inicial vai ser , que é a energia que encontramos no passo anterior. O trabalho é o produto da força pelo deslocamento (), assim colocando tudo isso na fórmula temos:
Onde é a energia cinética na base da pista, é a energia potencial gravitacional no topo da pista e é a energia dissipada pelo atrito. Como a altura é , a massa da esquiadora é e o trabalho realizado pelo atrito é , podemos calcular a velocidade dela a partir da expressão da energia cin��tica:
Para não se confundir com o sinal do trabalho, lembra que retira energia do movimento:
Passo 3
Lembrando que essa força é contrária ao movimento, por isso o sinal negativo.