Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 1.Problemas Adicionais - Ex. 38
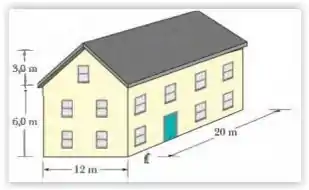
Nos Estados Unidos, uma casa de boneca tem uma escala de em relação a uma casa de verdade (ou seja, cada distância na casa de boneca é da distância correspondente na casa de verdade) e uma casa em miniatura (uma casa de boneca feita para caber em uma casa de boneca) tem uma escala de em relação a uma casa de verdade. Suponha que uma casa de verdade (Fig. 1-7) tenha de comprimento, de largura, de altura, e um telhado inclinado padrão (com o perfil de um triângulo isósceles)de de altura. Qual é o volume, em metros cúbicos,
(a) da casa de bonecas?
(b) da casa em miniatura correspondente?
Passo 1
Bom galera , a boa desse exercício é calculo o volume da casa real e utilizar este para determinar o volume das miniaturas. Podemos separar a casa real em 2 figuras sólidas conhecidas ( prisma retangular e paralelepípedo retângulo) . O volume do prisma triangular pode ser obtido através da relação :
O volume do paralelepípedo retângulo , por sua vez , pode ser obtido através das fórmula :
Logo ,
Passo 2
Beleza ,galera! Agora que sabemos o volume da casa real tudo fica mais fácil. Só precisamos multiplicar pela razão de proporção para ficarmos na escala certa .
Observem que a razão de proporção é linear , ou seja , de primeira ordem. E a conversão que pretendemos fazer é de terceira ordem , portanto , devemos multiplicar pelo razão de proporção elevada ao cubo :
Passo 3
Resolveremos o segundo item de forma análoga ao primeiro , porém com escalas diferentes:
É isso , galera!!! Partiu fazer mais exercícios???
Resposta
Ei, a resposta está no passo a passo :)