Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 1.6 - Ex. 19

Suponha que você esteja deitado na praia, perto do Equador, vendo o Sol se pôr em um mar calmo, e ligou um cronômetro no momento em que o Sol desaparece. Em seguida, você se levanta, deslocando os olhos para cima de uma distância   H = 1,70   m , e desliga o cronômetro no momento em que o Sol volta a desaparecer. Se o tempo indicado pelo cronômetro é t = 11,1   s , qual é o raio da Terra?

Passo 1

Bom galera , esse é um daqueles exercícios que dão medo , mas vamos tentar fazer de forma organizada para conseguirmos matar essa questão. Vejam um esquema do que está acontecendo :

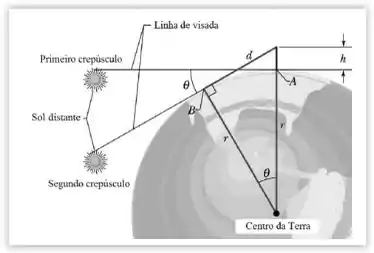
Quando o sol desaparece pela primeira vez , a sua linha de visão está tangente á superfície da terra no ponto A. Após nos levantarmos, nossos olhos sobem para uma altura h e a linha de visada passa a ser tangente à superfície da terra no ponto B .

Consideremos d a distância do ponto B até os seus olhos , então , utilizando o teorema de pitágoras no seguinte triângulo:

d 2 +   r 2 =   r + h 2

d 2 +   r 2 = r 2 +   2   r h + h 2

d 2 = 2 r h + h 2

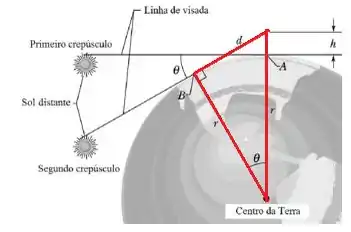
Além disso, nós sabemos que r   é     m u i t o   m a i o r   q u e   h , pois estamos tratando de distâncias que envolvem o raio da Terra. Dessa forma o segundo termo “   h 2   ” se torna praticamente desprezível , sendo assim :

d 2   ≅ 2 r h

Tranquilo até agora? Vamos que ainda não acabou!

Passo 2

Então pessoal observem que o ângulo entre as duas tangentes descrito como θ . Parando para analisar o ângulo coincide com o ângulo da trajetória que o sol realizou em relação a terra no período de tempo de 11,1   s . Desse modo podemos estabelecer uma relação entre o tempo de rotação da terra com ângulo θ . O ângulo θ   c o m p l e t a   360 °   e m   24 h . Com isso podemos montar a expressão que nos permite encontrar o ângulo θ no tempo de   t = 11,1 s :

θ 360 ° = t 24 h

Precisamos apenas colocar o tempo de 24h em segundos para não haver erros de conta.

θ 360 = 11,1   s 24 h × 60 m i n h × 60 s m i n

θ = 360 × 11,1 ( 86400 )

θ = 0,04625 °

Passo 3

Pronto, agora que achamos θ tudo fica mais fácil. Sabemos, a partir daquele triângulo retângulo do Passo 1 que:

t a n   θ =   c a t e t o   o p o s t o c a t e t o   a d j a c e n t e = d r  

Logo ,

d = r * t a n   θ   (1)

Voltando à questão, No Passo 1 concluímos que d 2   ≅ 2 r h . Podemos elevar a equação (1) ao quadrado e substituir o valor de d²:

d 2 = r * t a n   θ   2

d 2 = r 2 * ( t a n θ ) ²  

2 r h = r 2 * ( t a n θ ) ²  

Então, isolando o r na equação temos:

r = 2 h ( t a n θ ) ²  

Agora só precisamos substituir o h = 1,70 m que foi dado no enunciado

e o t a n θ = tan ⁡ 0,04625 º = 0,0008072 que você obtêm usando sua calculadora.

Assim, obtemos:

r = 5,2 × 10 6   m

Resposta

r = 5,2 * 10 6   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois tipos de barris foram usados como unidades de volume na década de 1920 nos Estados Unidos. O barril de maçã tinha um volume oficial de 7056 polegadas cúbicas; o barril de cranberry, 5826 polegada
A razão milho-porco é um termo financeiro usado no mercado de porcos, provavelmente relacionado ao custo de alimentar um porco até que ele seja suficientemente grande para ser vendido. É definida como
Os degraus de uma escada têm 19 cm de altura e 23 cm de largura. As pesquisas mostram que a escada será mais segura na descida se a largura dos degraus for aumentada para 28c m . Sabendo que a altura
Você foi encarregado de preparar um jantar para 400 pessoas em um encontro de apreciadores de comida mexicana. A receita recomenda usar duas pimentas jalapeño em cada porção (uma porção por pessoa). E
O vinho de uma grande festa de casamento será servido em um deslumbrante vaso de vidro lapidado com dimensões internas de 40c m × 40c m × 30c m( a l t u r a ) . O vaso deve ser enchido até a borda. O