Um estudante universitário propôs a seguinte expressão para a função de onda de uma partícula livre de massa m (uma partícula para qual a função energia potencial é igual a zero): e , onde é uma constante positiva. a)Faça um gráfico da função de onda proposta. b)Mostre que a função de onda proposta satisfaz a equação de Schrödinger para se a energia for dada por , ou seja, quando a energia da partícula for negativa. c)Mostre que a função de onda proposta também satisfaz a equação de Schrödinger para com a mesma energia do item (b). d)Explique por que, embora ela preencha essas condições, ela não é uma solução aceitável para equação de Schrödinger de uma partícula livre. (Sugestão: qual é o comportamento da função no ponto ?) Sabemos que é impossível uma partícula livre (aquela cuja a energia potencial possuir energia negativa.
Passo 1
letra a)
Na região , a função de onda cresce exponencialmente. Já na região , a função de onda decresce exponencialmente.
Além disso, terá um pico em .
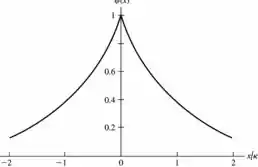
Passo 2
letra b)
A equação de Schrödinger para uma partícula livre é:
Para ver se a função é solução, basta substituirmos a função na equação.
Passo 3
Então a função dada será solução se:
Passo 4
letra c)
Vamos agora testar se a função para é solução também.
Então a função dada será solução se:
Passo 5
letra d)
Pelo o gráfico que fizemos da função no item (a), vemos que não é continua em .
Resposta
letra a)
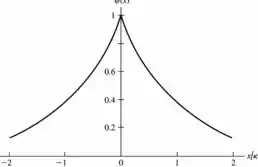
letra d) não é continua em .