Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 40.Problemas - Ex. 39

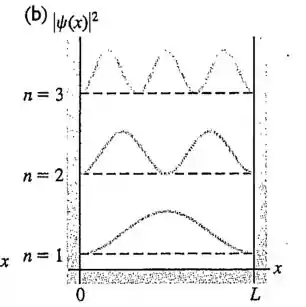
Qual é a probabilidade de se encontrar uma partícula em uma caixa de comprimento L em uma região entre x = L / 4 e x = 3 L / 4 quando a partícula está a)no nível fundamental? b) no primeiro nível excitado? (Sugestão: integre Ψ ( x ) 2 d x onde Ψ é normalizada, desde x = L / 4 até x = 3 L / 4 . ) c) Os resultados encontrados no itens (a) e (b) estão de acordo com a figura? Explique.

Passo 1

Para uma partícula em uma caixa :

Ψ ( x ) 2 = C 2 s e n 2 n π x L

Como está normalizada:

Ψ ( x ) 2 = 2 L s e n 2 n π x L

Para achar a probabilidade, precisamos integrar a norma da função de onda no intervalo dado no enunciado.

Passo 2

letra a)

A probabilidade desde x = L / 4 até x = 3 L / 4 será no estado fundamental será:

P = ∫ L / 4 3 L / 4 2 L s e n 2 π x L   d x

P = 2 L ∫ L / 4 3 L / 4 1 - c o s 2 π x L 2   d x

P = 1 L x - L 2 π s e n 2 π x L L / 4 3 L / 4

P = 1 L 3 L 4 - L 4 - - L 2 π - L 2 π

P = 1 2 + 1 π

Passo 3

letra b)

A probabilidade desde x = L / 4 até x = 3 L / 4 no primeiro estado excitado será:

P = ∫ L / 4 3 L / 4 2 L s e n 2 2 π x L   d x

P = 2 L ∫ L / 4 3 L / 4 1 - c o s 4 π x L 2   d x

P = 1 L x - L 4 π s e n 4 π x L L / 4 3 L / 4

P = 1 L 3 L 4 - L 4 - 0

P = 1 2

Passo 4

letra c)

Esses resultados são consistentes com a figura. Essa figura mostra que Ψ ( x ) 2 é mais

concentrado próximo ao centro da caixa para o estado fundamental do que para o primeiro estado excitado; isso é consistente com a resposta da parte (a) que é maior que a resposta da parte (b). Além disso, esta figura mostra que, para o primeiro estado excitado, metade

a área sob a curva Ψ ( x ) 2 lies fica entre x = L / 4 até x = 3 L / 4 , consistente com a nossa resposta da parte (b).

Resposta

letra a) P = 1 2 + 1 π

letra b) P = 1 2

letra c) são consistentes com a figura.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exercício de Livro
Exercício de Livro
Uma partícula está confinada em uma caixa com paredes rígidas entre x = 0 e x = L . Embora o módulo da força instantânea que a parede exerce sobre a partícula seja igual a infinito e o tempo de atuaçã
A distância de penetração η em um poço de potencial finito é a distância em que a função de onda diminui a 1 / e da função de onda no ponto clássico da inversão: Ψ ( x = L + η ) = 1 e Ψ ( L ) Pode-se
Fóton em um laser de corante. Um elétron em uma longa molécula orgânica usada em um laser de corante se comporta aproximadamente como uma partícula em uma caixa de largura igual a 4,18n m . Qual é o c