Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 52

Para evitar lesionar os ombros, sua idosa avó deseja comprar o batedor de tapetes com o menor momento de inércia em relação à empunhadura. Sabendo que você estuda física, ela solicita seu conselho. Há dois modelos para escolher. O modelo A tem um cabo de 1,0 m que termina em um quadrado de 40 c m de lado, as massas do cabo e do quadrado sendo 1,0 k g e 0,5 k g , respectivamente. O modelo B tem um cabo de   0,75 m que termina em um quadrado de 30 c m de lado, as massas do cabo e do quadrado sendo 1,5 k g e 0,6 k g , respectivamente. Qual é o modelo que você recomenda? Determine qual é o batedor mais fácil de manejar, da empunhadura, calculando o momento de inércia dos dois.

Passo 1

Falaaaa, querido!

A gente tem nossa vozinha querida que quer saber qual batedor é mais fácil para ela usar. E para descobrir, a gente vai calcular o momento de inércia desses dois modelos em relação a um eixo que passa pela extremidade do cabo (onde ocorre a rotação durante o uso).

Aí o modelo que tiver o menor momento de inércia vai ser o melhor para nossa vó, tudo bem?

Bora lá!

Passo 2

Bem, o batedor A é formado por um cabo e um quadrado na ponta. Desse jeitinho:

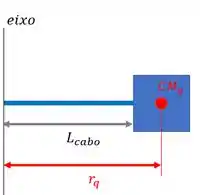
O momento de inércia do batedor em relação ao eixo mostrado vai ser a soma do momento de inércia do cabo com o momento de inércia do quadrado.

I = I c a b o + I q u a d r a d o

O momento de inércia do cabo é o momento de inércia de uma barra final em relação a um eixo que passa por sua extremidade. Ele tem essa fórmulinha:

I c a b o = m c L 2 3

Onde L é o comprimento do cabo, que vale L = 1   m e m c = 1   k g , a massa do cabo.

Já o momento de inércia do quadrado a gente pode aproximar como o momento de inércia de uma partícula em relação a um eixo. Ele tem essa fórmulinha:

I q u a d r a d o = m q r 2

Onde m q = 0,5   k g a massa do quadrado e r é a distância entre o eixo do momento de inércia e o centro de massa do quadrado (que fica no centro dele). Esse r vai valer então:

r = 1 + 0,4 2 = 1,2   m

Passo 3

Então o momento de inércia do batedor de modelo A é

I = I c a b o + I q u a d r a d o

I A = m c L 2 3 + m q r 2

Substituindo os dados:

I A = 1 × 1 2 3 + 0,5 × 1 , 2 2

I A = 1.05   k g ⋅ m 2

Passo 4

O modelo B tem a mesma geometria do modelo A. Então temos novamente:

I = I c a b o + I q u a d r a d o

O que muda são só as medidas, ou seja, nossas variáveis das fórmulinhas. Para o cabo:

I c a b o = m c L 2 3

Onde L é o comprimento do cabo, que agora vale L = 0,75   m e m c = 1 , 5   k g , a massa do cabo.

Já o momento de inércia do quadrado, que a gente pode aproximar como uma partícula, fica:

I q u a d r a d o = m q r 2

Onde agora m q = 0 , 6   k g a massa do quadrado e r é a distância entre o eixo do momento de inércia e o centro de massa do quadrado (que fica no centro dele). Esse r vai valer então:

r = 0,75 + 0 , 3 2 = 0,75 + 0,15

Passo 5

Então o momento de inércia fica:

I = I c a b o + I q u a d r a d o

I B = m c L 2 3 + m q r 2

Substituindo os valores:

I B = 1.5 × 0.75 2 3 + 0.6 × 0.75 + 0.15 2

I B = 0.77   k g ⋅ m 2

Como o modelo B tem momento de inércia menor, ele é o mais adequado para a vovó.

Resposta

I A = 1.05   k g ⋅ m 2

I B = 0.77   k g ⋅ m 2

Como o modelo B tem momento de inércia menor, ele é o mais adequado para a vovó.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas barras finas (ambas de massa 0,2 k g ) estão unidas para formar um corpo rígido como mostra a figura abaixo. Uma das barras tem comprimento L 1 = 0,4 m e a outra tem comprimento L 2 = 0,5 m . Qua
A barra fina e homogênea da Fig. 10-50 tem 2,0m de comprimento e pode girar, sem atrito, em torno de um pino horizontal que passa por uma das extremidades. A barra é liberada a partir do repouso e de
(a) Mostre que o momento de inércia de um cilindro maciço de massa M e raio R em relação ao eixo central é igual ao momento de inércia de um aro fino de massa M e raio R / 2 em relação ao eixo central
Um corpo rígido é formado por três barras finas iguais, de comprimento L=0,600m , unidas na forma da letra H (Fig. 10-49). O corpo pode girar livremente em torno de um eixo horizontal que coincide com
Use integração para determinar o momento de inércia, em relação ao seu eixo, de um cone circular reto uniforme de altura H , raio da base R e massa M .