A barra fina e homogênea da Fig. 10-50 tem de comprimento e pode girar, sem atrito, em torno de um pino horizontal que passa por uma das extremidades. A barra é liberada a partir do repouso e de um ângulo acima da horizontal. Use a lei de conservação da energia para determinar a velocidade angular da barra ao passar pela posição horizontal.
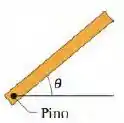
Passo 1
Vamos lááá!!!! Queremos determinar a velocidade angular na barra ao passar pela posição horizontal...
Beleza, a primeira coisa que podemos fazer aqui é calcular a altura que o centro de massa está quando a barra é liberada:

Logo:
Passo 2
Assim, a energia potencial inicial correspondente é dada como:
Essa energia é convertida em energia cinética de rotação em relação ao pino, dada como:
Em que é o momento de inércia da barra em relação ao pino, ou seja, temos uma barra que gira em torno de um eixo em uma de suas extremidades, sendo assim seu momento de inércia é tabelado e dado pra gente como:
Logo:
Como a energia potencial se transforma na energia cinética, pela conservação temos que:
Isolando , vamos obter que:
Susbituindo os valores do enunciado:
