Use integração para determinar o momento de inércia, em relação ao seu eixo, de um cone circular reto uniforme de altura , raio da base e massa .
Passo 1
Oláaa, cê está bem? Ele quer o momento de inércia de um cone maciço em relação ao seu eixo.
Como o enunciado diz, já sabemos que vamos precisar integrar pra achar o momento de inércia. Já que o cone tem seções horizontais circulares, em vez de a gente calcular o momento de inércia pela definição:
A gente vai dividir esse cone em discos de massa e raio , onde varia com a altura do cone:
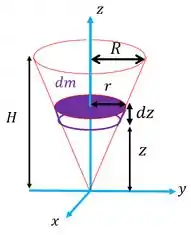
Esses discos são muuuito fininhos, eles tem espessura . Por isso, a gente considera que o raio deles é constante em relação a essa espessura e vale . (no desenho o disco não é tão fino, mas é mais para gente poder enxergar mesmo hehe)
Agora vamos ver como usar eles para achar o nosso momento de inércia do cone. Bora!
Passo 2
Por que gente faz essa divisão do cone em discos? Porque a gente sabe a fórmula do momento de inércia de um disco em relação a um eixo que passa pelo seu centro (é igual ao do cilindro maciço):
Então se nosso disco tem raio e massa , o momento de inércia dele vai ser:
Aí para achar o momento de inércia do cone inteiro, a gente soma todos os de todos os discos usando uma integral:
A ideia é a gente montar essa integral e calcular.
Passo 3
Precisamos reescrever essa . Podemos usar a massa específica do cone. Como? Ela é dada por
Sendo que é constante, então um disco nosso também vai ter essa massa específica. Logo, podemos escrever:
E é o volume do disco, que é área da base vezes a espessura :
Então a massa do disco é:
Substituindo na integral:
Passo 4
Agora repara que a nossa integral é em relação a variável . Então a gente precisa colocar em função de .
Lembra que o raio de um disco varia com a altura do cone, ou seja, é uma função de ? Então vamos achar essa relação entre e . A gente pode usar semelhança de triângulos. Temos esse triângulo contido no cone:
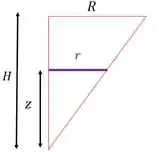
Por semelhança:
Subsituindo na integral:
Passo 5
Como é a altura, o valor máximo dele é e o mínimo é (altura do cone), então nossos extremos de integração são
E aí momento de inércia do cone é calculado como:
Tirando o que é constante da integral
Usando a regrinha de integrar polinômios e arrumando o resultado:
Passo 6
Mas repara que não temos , mas a gente sabe que
E o volume de um cone é um terço do produto entre a altura dele e área da base:
Então fica:
Substituindo no nosso :
Simplificando: