Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 38
No Exemplo 13-3, uma força de 150 N é aplicada sobre um pistão pequeno para levantar um carro que pesa 15000 N. Demonstre que isto não viola a lei de conservação da energia mostrando que, quando o carro é elevado de uma distância h, o trabalho realizado pela força de 150 N que atua sobre o pistão pequeno é igual ao trabalho realizado sobre o carro pelo pistão grande.
Passo 1
Fala, querido! Vamos lembrar do que o exemplo 13-3 falava. Tínhamos um elevador hidráulico. No pistão maior, de raio tínhamos um carro que pesava , e para levantar esse carro, teríamos que aplicar uma força de no pistão menor de raio igual a .
Desenhando a situação:
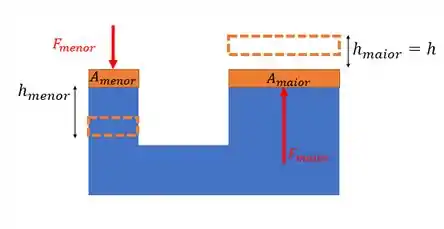
O enunciado quer que a gente prove que esse resultado não viola a conservação de energia, mostrando que o trabalho realizado pelas forças é igual. Aqui, vamos usar o conceito de trabalho realizado por uma força, ou seja:
Neste caso, para suspender o carro de uma altura , a força que está sendo aplicada pelo fluído no pistão maior e que vale deve produzir o trabalho
A ideia aqui é a gente provar que o trabalho realizado pela força menor é o mesmo.
Vamos fazer isso usando o princípio de Pascal que foi usado no exemplo descrito. Vem ver como fica!
Passo 2
Bom, vamos lá! Pelo princípio de Pascal temos que a variação na pressão em um lado será igual para todos os pontos do fluindo, sendo assim a pressão no pistão maior é igual a pressão no pistão menor
Lembrando que:
Podemos reescrever as pressões
Isolando a força menor, da qual a gente quer descobrir o trabalho
Passo 3
Agora, quando nós temos um fluido incompressível em um ambiente fechado, ao deslocar o volume de um dos lados, consequentemente, o outro lado terá a mesma variação:
Lembrando que:
Isolando a altura menor, que vai ser o deslocamento da força menor:
Passo 4
Falta pouco! Já sabemos a fórmula do trabalho:
Então para a força menor:
Substituindo as expressões que achamos para e :
Agora lembra que é e o deslocamento do pistão maior é :
E isso é exatamente igual a expressão que achamos para o trabalho da força menor 😉
Resposta
Ei, a resposta está no passo a passo :)