Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 22.Exercícios - Ex. 4.b
. No Exemplo , verificamos que o campo elétrico produzido por um fio retilíneo infinito carregado é perpendicular ao fio e possui módulo . Considere
uma superfície cilíndrica imaginária de raio e comprimento , com uma carga positiva distribuída uniformemente sobre seu comprimento. A carga por unidade de
comprimento sobre a linha é .
Qual é o fluxo elétrico através do cilindro quando seu raio aumenta para ?
Passo 1
Vem comigo que a gente detona essa questão juntos!
Nesse problema temos uma superfície cilíndrica de comprimento que envolve o fio da seguinte maneira:
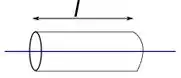
Para calcular o fluxo pelo cilindro do campo gerado pelo fio vamos usar a seguinte equação que nos fornece o fluxo do campo elétrico através de uma superfície:
A superfície cilíndrica é composta pelas tampas e pelo o tudo, o elemento de área das tampas é perpendicular ao campo elétrico gerado pelo fio que é radial, logo:
O elemento de área do tubo que compõe o cilindro é paralelo ao campo elétrico, logo:
Então temos que o fluxo é dado da seguinte forma:
Como o campo é homogêneo por todo o espeço, temos que:
Passo 2
A integral do elemento de área que chegamos no passo , nada mais é do que a área do tubo do cilindro, logo:
Então temos que o fluxo do campo do fio no cilindro é:
Passo 3
O enunciado nos deu a expressão para o campo do fio, então temos que:
Como a gente pode ver o fluxo não depende do valor do raio do cilindro. Substituindo os valores que conhecemos, temos:
Questão finalizada com sucesso!