Na experiência do esplho de Lloyd, observa-se num anteparo O a interferência entre a luz que vai diretamente de uma fonte puntiforme F para um ponto P do anteparo O e a luz que vai de F para P refletindo-se numa placa plana de vidro E (fig.). A distância de F ao plano da placa é d e a distância de F a O é D ≫ d . Observa-se a primeira franja brilhante (máximo) de interferência num ponto P a uma distância y do plano da placa, usando luz monocromático de comprimento de onda λ . Calcule y em função de λ , d e D .Sugestão: Considere a imagem especular de F e a defasagem na reflexão.

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 3.Problemas - Ex. 1

Na experiência do esplho de Lloyd, observa-se num anteparo a interferência entre a luz que vai diretamente de uma fonte puntiforme para um ponto do anteparo e a luz que vai de para refletindo-se numa placa plana de vidro (fig.). A distância de ao plano da placa é e a distância de a é . Observa-se a primeira franja brilhante (máximo) de interferência num ponto a uma distância do plano da placa, usando luz monocromático de comprimento de onda . Calcule em função de , e .

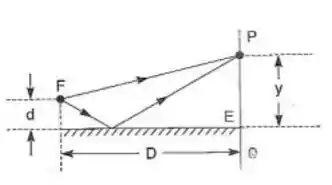
Sugestão: Considere a imagem especular de e a defasagem na reflexão.

Passo 1

Esse é um exercício bem legal de fazer! Dois raios de luz, que percorrem trajetórias diferentes, vão interferir um com o outro no ponto . Queremos saber a posição do ponto onde ocorrer o primeiro máximo!

Vamos seguir a sugestão dada no enunciado: considerar a imagem especular de sobre o espelho:

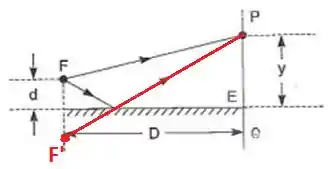
(Imagem adaptada do livro)

Note que podemos analisar o caminho da luz que sai de , reflete no espelho e chega até como se ela saísse de e fosse direto para . Com isso, como é pequeno, podemos pensar em e como duas fendas separadas por uma distância . Sendo assim, a diferença de caminho ótico percorrido pelos dois raio é

Observem como esse truque é genial: achamos a diferença de caminha fazendo apenas uma analogia com o caso da fenda dupla!

Passo 2

Nós sabemos que no geral, a defasagem é dada por

Mas só usamos essa expressão se a única fonte de defasagem for a diferença de caminho. Nesse caso, além da diferença de caminho, temos que considerar uma defasagem de devido à reflexão que um dos raios sofre entre um meio com e outro meio com . Portanto,

Logo,

Para que a interferência seja construtiva, devemos ter

Ou seja, a defasagem deve ser um múltiplo inteiro de . Logo,

Portanto,

Passo 3

Como os ângulos são pequenos, temos que

Assim,

Como queremos o primeiro máximo, fazemos :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

49. Na Figura 35.3 , suponha que as fontes S 1 e S 2 estejam localizadas nos pontos y = d e y = - d , respectivamente. a ) Rescreva a Equação ( 35.1 ) em termos das coordenadas x e y em um ponto P da

Dois alto-falantes emitindo ondas sonoras idênticas de comprimento de onda igual a 2m em fase uma com a outra e um observador estão posicionados como mostra a Figura 35.21. a) No local onde está o obs

Os campos elétricos recebidos em um ponto P de duas fontes coerentes e idênticas são dados por E 1 ( t ) = E c o s ( ω t + c ) e E 2 ( t ) = E c o s ( ω t ) . a) Aplique uma das identidades trigonomét