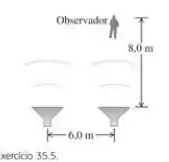
Dois alto-falantes emitindo ondas sonoras idênticas de comprimento de onda igual a 2m em fase uma com a outra e um observador estão posicionados como mostra a Figura 35.21. a) No local onde está o observador, qual é a diferença entre os caminhos das ondas provenientes dos dois alto-falantes? B) As ondas sonoras irão interferir construtivamente ou destrutivamente no local onda está o observador? Ou será uma interferência entre construtiva e destrutiva? C) Suponha que o observador agora amplie a sua distância dos alto-falantes para 17m, permanecendo diretamente na frente do mesmo alto-falante como inicialmente. Responda as questões a) e b) para essa nova situação.
Passo 1
a) Faala ae, beleza?? Bora resolver esse probleminha de óptica física.
Então, como na imagem mostra, temos dois alto-falantes separados por 6m e uma pessoa a 8 metros diretamente acima de um desses alto-falantes, vamos chamar esse de alto-falante 2, ok? Logo, o outro será o alto-falante 1.
Então, para saber a diferença de caminho entre as ondas dessas duas fontes, vamos recorrer à trigonometria! Podemos contruir um triângulo retângulo com as fontes e o observador, assim:
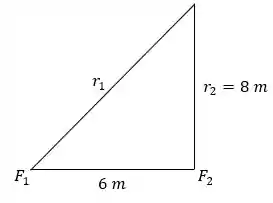
Onda e são as posições das fontes 1 e 2.
Dessa forma, vemos que a distância da fonte 1 até o observador pode ser calculada por Pitágoras:
Passo 2
Beleza!! Então, como o comprimento de onda vindo das fontes é 2m, temos as distâncias:
Onde , que é o comprimento de onda, ok??
Show, nossa diferença de caminho será:
Passo 3
b) Opa, esse último resultado nos deu a resposta dessa letra já!! Pois temos que se a diferença de caminho é um múltiplo inteiro de comprimentos de onda, a interferência no ponto será construtiva! Lembra?
Para interferência construtiva temos que:
Onde . No nosso caso, temos que .
Passo 4
c) Agora, se o observador passa a ficar 17 m distante da fonte 2, temos essa situação:
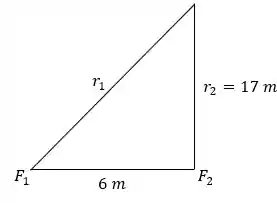
Assim, temos que:
Com isso, seguindo sempre o mesmo raciocínio que usamos nas duas letras anteriores:
E nossa diferença de caminho será:
Essa seria a resposta da (a) nessa nova situação.
Passo 5
Para a nova (b), vamos olhar para o número que está multiplicando no resultado da diferença de caminho. Assim, vemos que temos um múltiplo não-inteiro, . Dessa forma, a interferência nesse novo ponto será destrutiva.
Pois, relembrando, a interferência destrutiva ocorre quando a diferença de caminho é um número semi-inteiro de comprimentos de onda:
Onde No nosso caso, temos que, ficando dentro dos parênteses. Beleza?? Só isso! 😊
Resposta
(a)
(b) Construtiva
(c) , destrutiva.