Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 21.Exercícios - Ex. 11
Em um experimento no espaço, um próton é mantido fixo e outro é liberado do repouso a uma distância de .
(a) Qual é a aceleração inicial do próton após ser liberado?
(b) Faça gráficos qualitativos (sem números!) de aceleração versus tempo e velocidade versus tempo do movimento do próton liberado.
Passo 1
Olá, tudo bem? Vou ajudar você aqui!
Letra (a):
Aqui vou misturar a segunda lei de Newton com a lei de Coulomb.
Os dados que o problema nos dá são:
A aceleração pode então ser encontrada assim:
Usando a força elétrica:
Tranquilo?
Passo 2
Letra (b):
E agora como se comportam a aceleração e a velocidade? Bom, vamos começar pela velocidade. Como partimos do repouso, no instante inicial ela é zero e varia conforme a aceleração. No começo temos uma aceleração bem alta, mas e conforme a distância vai aumentando, acontece o que com ela?
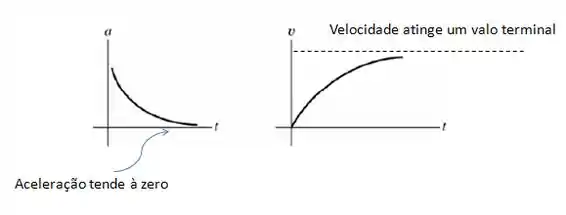
Dá uma olhada na expressão pra aceleração ali do passo anterior. A aceleração é inversamente proporcional à distância, sendo assim, à medida que o próton vai se afastando do outro (aqui a força é de repulsão, pois temos cargas iguais), a aceleração tende à zero.
E o que acontece com a velocidade? Bom, se a aceleração começa alta e vai diminuindo, a velocidade começa aumentando, mas com o passar do tempo assume um valor limite, quase constante (já que a aceleração é praticamente zero). Os gráficos que demonstram isso são esses aqui:
