Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.Problemas - Ex. 91

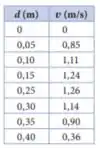
Em um experimento no laboratório de física, a extremidade de uma mola horizontal que obedece à lei de Hooke é presa a uma parede. A mola é comprimida por 0,400   m e o bloco, com massa de 0,300   k g , é preso a ela. A mola é então liberada, e o bloco se move ao longo de uma superfície horizontal. Sensores eletrônicos medem a velocidade v do bloco depois que ele tiver atravessado uma distância d de sua posição inicial contra a mola comprimida. Os valores medidos são listados na tabela. (a) Os dados mostram que a velocidade v do bloco aumenta e depois diminui à medida que a mola retorna a seu comprimento original. Explique por que isso acontece, em termos do trabalho realizado sobre o bloco pelas forças que atuam sobre ele. (b) Use o teorema do trabalho-energia para derivar uma expressão para v 2 em termos de d . (c) Use um programa gráfico (por exemplo, Excel ou Matlab) para representar os dados como v 2 (eixo vertical) versus d (eixo horizontal). A equação que você derivou na parte (b) deverá mostrar que v 2 é uma função de segundo grau de d ; portanto, no seu gráfico, ajuste os dados por um polinômio de segundo grau (quadrático) e faça com que o programa mostre a equação para essa linha de tendência. Use essa equação para achar a velocidade v máxima do bloco e o valor de d no qual essa velocidade ocorre. (d) Comparando a equação do programa gráfico com a fórmula que você derivou no item (b), calcule a constante de força k para a mola e o coeficiente de atrito cinético para a força de atrito que a superfície exerce sobre o bloco.

Passo 1

Fala galerinha, beleza?

Esse é um exercício mais complicadinho porque envolve dados e uma interpretação bem detalhada da situação, além da construção de um modelinho para descrever o problema.

Seja Δ x a deformação da mola. Quando Δ x < 0 , a mola está comprimida. Já para Δ x > 0 , a mola está esticada. A força elástica restauradora que a mola faz sobre o bloco é

F = - k   Δ x

Vamos tentar escrever Δ x em termos da posição x do bloco. Na posição x = 0 (inicial), a deformação da mola é Δ x = - D , onde D = 0,400   m . Já quando x = D , a mola está relaxada, com Δ x = 0 . Com isso, parece razoável escrever

Δ x = x - D

Portanto,

F = - k x - D

O trabalho da força elástica entre a posição inicial x = 0 e uma posição arbitrária x = d é dado por

W F = ∫ 0 d F   d x = - k   ∫ 0 d x - D   d x = - k   x 2 2 - D x 0 d

Portanto,

W F = - k d 2 2 - D d = k D d - k 2 d 2

Passo 2

Já o trabalho do atrito é simplesmente

W F a t = - μ N d = - μ m g d

Com isso, podemos achar o trabalho total somando os trabalhos:

W = W F + W F a t = k D - μ m g   d - k 2 d 2

Daí, basta usar o teorema trabalho-energia:

W = K f - K i

Como a energia cinética inicial é nula, temos que

k D - μ m g   d - k 2 d 2 = 1 2 m v 2

Isolando v 2 , temos que

v 2 = - k m d 2 + 2 k D m - 2 μ g d

Para simplificar um pouco as coisas, vou escrever

v 2 = - A   d 2 + B   d ,               A = k m                     B = 2 k D m - 2 μ g

Portanto, nosso modelo prevê que v 2 seja uma função quadrática de d . No próximo passo vamos plotar os pontos da tabela e ver isso ocorre!

Passo 3

A tabela forneceu v como função de d . Vamos elevar as velocidades ao quadrado para ter os dados do jeito que a gente quer:

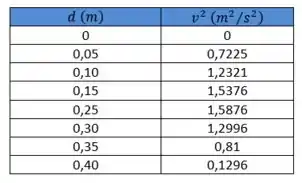
Bom, agora plotamos os pontos e ajustamos uma curva usando um software de ajuste:

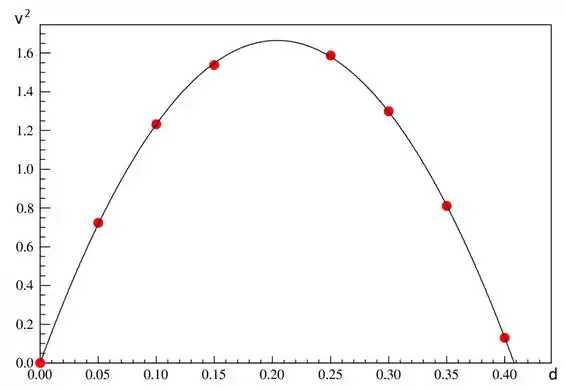
Os parâmetros A e B encontrados foram

A = 39,9863                 B = 16,3191

Para achar o valor máximo da curva, basta tomar a derivada da expressão de v 2 :

d d d v 2 = - 2 A d + B = 0 → d = B 2 A

Logo,

d = 16,3191 2 ⋅ 39,9863 = 0,204   m

A velocidade correspondente é

v m a x = - 39,9863 ⋅ 0,204 2 + 16,3191 ⋅ 0,204

Portanto,

v m a x = 1,29   m / s

Passo 4

Agora que temos A e B , podemos achar k e μ :

A = k m → k = m A

Logo,

k = 0,300 ⋅ 39,9863 → k = 11,99   N / m

Da mesma forma,

B = 2 k D m - 2 μ g → 2 μ g = 2 A D - B

Ou ainda,

μ = 2 A D - B 2 g = 2 ⋅ 39,9863 ⋅ 0,400 - 16,3191 2 ⋅ 9,8 → μ = 0,799

Resposta

v 2 = - k m d 2 + 2 k D m - 2 μ g d

v m a x = 1,29   m / s

k = 11,99   N / m

μ = 0,79 9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de gelo flutuante é colhido por uma correnteza que aplica ao bloco uma força F → = 210N i ^ - 150N j ^ , fazendo com que o bloco sofra um deslocamento d → = 15m i ^ - 12m j ^ . Qual é o traba
Um corpo de 3,0k g está em repouso sobre um colchão de ar horizontal de atrito desprezível quando uma força horizontal constante F → é aplicada no instante t = 0 . A Fig. 7-24 mostra, em um gráfico et
Uma criança assustada desce por um escorrega de atrito desprezível em um parque de diversões apoiada pela mãe. A força da mãe sobre a criança é de 100N para cima ao longo do escorrega e a energia ciné
Considere o sistema indicado na Figura 6.26. A corda e a polia possuem massas desprezíveis, e a polia não tem atrito. Inicialmente o bloco de 6,00 kg está se deslocando verticalmente para baixo e o bl
Uma aluna de física gasta parte do seu dia caminhando para se deslocar entre salas de aula ou durante os intervalos e, nesse período, ela gasta energia com uma taxa média de 280 W. No restante do dia