O potencial elétrico é o mesmo em todos os pontos na superfície de um condutor. Isto significa que a densidade superficial de cargas é também a mesma em todos os pontos da superfície? Explique sua resposta?
Passo 1
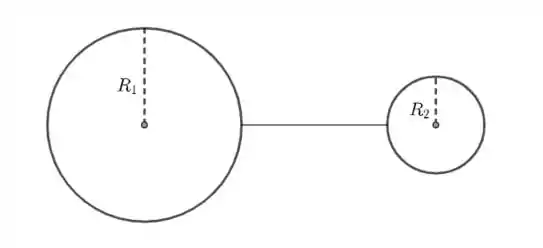
Falaa galera, beleza? Essa pergunta é bastante abstrata, não concorda? Então, vamos aplicar uma situação em específico que é ligar duas esferas por um fio metálico. Suponha que essas esferas possuem raios diferentes. Veja a figura a seguir:
Passo 2
Essa situação parece bem diferente da proposta do enunciado, né? Mas o que acontece é o seguinte: quando a gente liga dois corpos condutores por um fio ideal, é como se eles virassem apenas um condutor, pois a função do fio é justamente igualar o potencial das esferas.
Assim, suponha que a esfera possua carga e a esfera possua carga . Como o potencial das esferas devem ser iguais, segue que:
Como queremos saber da densidade superficial de cargas, vamos multiplicar os dois denominadores por (lembre-se que a área da esfera é ). Segue que
Para obtermos a área de cada esfera, façamos o seguinte:
Porém, é justamente (densidade superficial de cargas da esfera 1). Da mesma maneira, temos . Dessa forma,
Passo 3
Porém, como , segue que , segue que
ou seja, a densidade da esfera maior é menor... isso indica que, mesmo em condutores com o mesmo potencial elétrico, a densidade de carga vai mudando... e mais: a densidade é maior em regiões mais agudas (menor raio de curvatura). Tal fenômeno é conhecido como poder das pontas e isso explicas, em partes, o funcionamento do para raios.
Passo 4
Voltando para a pergunta, podemos imaginar o condutor como sendo um monte de esferinhas ligadas uma na outra... assim, como vimos acima, a densidade superficial de cargas irá mudar! E será maior em regiões com menor raio de curvatura.
Resposta
A densidade varia.