Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 29.1 - Ex. 41

A Figura 29-33 mostra um resistor com resistencia de carga conectado a um filtro passa-altas constituído por um indutor com indutancia e um resistor com resistencia . A saida do gerador ac idealedada por = ( 100 V ) c o s ⁡ ( 2 π f t ) . Determine as correntes rms em todos os três ramos do circuito se a freqiienciae(a)500 Hz e(b)2000 Hz.Determine a fracao da potencia media total fornecida pelo gerador ac que eentregue ao resistor de carga se a frequiencia e(c)500 Hz. e(d)2000 Hz

Passo 1

E ai galera!! Vamos começar aqui essa questão?? Vai ser bem rápido e eu garanto que vocês vão entender!!

ε = V 1 + V 2 , onde V 1 é a queda de tensão em R e V 2 é a queda de tensão na combinação paralela de L e R L . ε → = V → 1 + V → 2 é a relação para os fasores. Para a combinação paralela   I → = I → R i + I → L . Além disso, V 1 está em fase com I e V 3 está em fase com I R L . Primeiro, desenhe o diagrama fasorial para as correntes na combinação paralela e, em seguida, adicione os fasores para as tensões ao diagrama.

O diagrama fasorial para as correntes no circuito é:

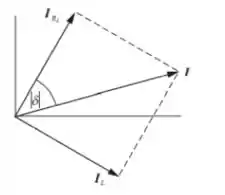
Adicionar os fasores de tensão ao diagrama nos dá:

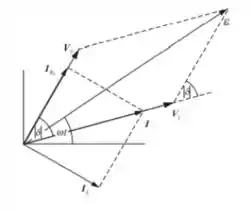
Passo 2

A corrente máxima no indutor, I 2 ,   p i c o , é dada por:

I 2 ,  pico  = V 2 ,  pico Z 2             ( 1 )   o n d e     Z 2 - 2 = R L - 2 + X L - 2             ( 2 )

t a n | δ | é dado por:

t a n ⁡ | δ | = I L ,  pico  I R ,  pico = V 2 ,  pico X L V 2 ,  pico R L = R L X L = R L ω L = R L 2 π t

Resolva para | δ | para obter:

δ = tan - 1 ⁡ R L 2 π f L                           ( 3 )

Aplique a lei dos cossenos ao triângulo formado pelos fasores de tensão para obter:

ε pico  2 = V 1 ,  pico 2 + V 2 ,  pico 2 + 2 V 1 ,  pico V 2 ,  pico cos ⁡ δ

Ou

I pico  2 Z 2 = I pico 2 R 2 + I pico 2 Z 2 2 + 2 I pico R I pico Z 2 c o s ⁡ | δ |

Dividindo a corrente ao quadrado, temos:

Z 2 = R 2 + Z 2 2 + 2 R Z 2 c o s ⁡ | δ |

Resolvendo Z:

Z = R 2 + Z 2 2 + 2 R Z 2 c o s ⁡ | δ | (4)

A corrente máxima I p i c o no circuito é dado por:

I pico  = ε pico Z (5)

I r m s está relacionado a I p i c o de acordo com:

I m s = 1 2 I pico                   ( 6 )

Passo 3

Letra a:

Substitua os valores numéricos na equação (3) e avalie | δ | :

| δ | = t a n - 1 ⁡ 20.0 Ω 2 π 500 H z 3.20 m H = t a n - 1 ⁡ 20.0 Ω 10.053 Ω = 63.31 ∘

Resolvendo a equação (2) para Z 2 , temos:

Z 2 = 1 R L - 2 + X L - 2

Substitua os valores numéricos e avalie Z 2 :

Z 2 = 1 ( 20.0 Ω ) - 2 + ( 10.053 Ω ) - 2 = 8.982 Ω

Substitua os valores numéricos e avalie Z:

Z = ( 4.00 Ω ) 2 + ( 8.982 Ω ) 2 + 2 ( 4.00 Ω ) ( 8.982 Ω ) c o s ⁡ 63.31 ∘ = 11.36 Ω

Substitua os valores numéricos na equação (5) e avalie I p i c o :

I pico  = 100 V 11.36 Ω = 8.806 A

Substitua por I p i c o na equação (6) e avalie I r m s :

I r m = 1 2 ( 8.806 A ) = 6.23 A

Os valores máximos e rms de V 2 são dados por:

V 2 ,  pico  = I pico Z 2 = ( 8.806 A ) ( 8.982 Ω ) = 79.095 V

E

V 2 , m s s = 1 2 V 2 ,  pico  = 1 2 ( 79.095 V ) = 55.929 V

Os valores rms de I R L , r m s são:

I R L , m k = V 2 , r m s R L = 55.929 V 20.0 Ω = 2.80 A   e I L , m s = V 2 , r m s X L = 55.929 V 10.053 Ω = 5.56 A

Passo 4

Letra b:

Proceda como na letra a, com f = 2000 H z para obter:

X L = 40.2 Ω , | δ | = 26.4 ∘ , Z 2 = 17.9 Ω Z = 21.6 Ω , I pico  = 4.64 A ,   e   I r m s = 3.28 A V 2 , m a x = 83.0 V , V 2 , r m s = 58.7 V I R l , m s = 2.94 A ,   a n d   I L , m s = 1.46 A

Passo 5

Letra c:

A potência fornecida pela fonte CA é igual à soma da potência dissipada nos dois resistores. A fração da potência total fornecida pela fonte que é dissipada no resistor de carga é dada por:

P R i P R L + P R = 1 + P R P R t - 1 = 1 + I m s 2 R I R L , m s 2 R L - 1

Substitua os valores numéricos por f = 500 H z para obter:

P R L P R l + P R f = 500 H z = 1 + ( 6.23 A ) 2 ( 4.00 Ω ) ( 2.80 A ) 2 ( 20.0 Ω ) - 1 = 0.502 = 50.2 %

Passo 6

Letra d:

Substitua os valores numéricos por f = 2000 H z para obter:

P R t P R t + P R f = 2000 H x = 1 + ( 3.28 A ) 2 ( 4.00 Ω ) ( 2.94 A ) 2 ( 20.0 Ω ) - 1 = 0.800 = 80.0 %

Resposta

  1. I R L , m k = V 2 , r m s R L = 55.929 V 20.0 Ω = 2.80 A   e I L , m s = V 2 , r m s X L = 55.929 V 10.053 Ω = 5.56 A
  2. X L = 40.2 Ω , | δ | = 26.4 ∘ , Z 2 = 17.9 Ω Z = 21.6 Ω , I pico  = 4.64 A ,   e   I r m s = 3.28 A V 2 , m a x = 83.0 V , V 2 , r m s = 58.7 V I R l , m s = 2.94 A ,   a n d   I L , m s = 1.46 A
  3. 50.2 %
  4. 80.0 %
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o circuito mostrado na Fig. 35-10. Com a chave S 1 , fechada e as outras duas chaves abertas o circuito tem uma constante de tempo τ C , (veja a Seção 29-8). Com a chave S 2 , fechada e as o
Um circuito LC consiste num indutor de 75.0 mH e num capacitor de 3,60 μ F.Sabendo-se que a carga máxima do capacitor é 2,90 μ C.(a) qual é a energia total no circuito e (b) qual é a corrente máxima?
Um circuito LC tem uma indutância de 3,00 mH e uma capacitância de 10,0 μ F Calcular (a) a frequência angular e ( b) o período de oscilação.(c) No instante t — 0. a carga do capacitor é de 200 μ C e a
Qual é o valor máximo de uma tensão alternada cujo valor rms è 100V ?
Use a regra das malhas para obter a equação diferencial de um circuito LC (Eq. 31-11).