Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 7
Faça um desenho para cada um dos seguintes vetores, depois obtenha seus componentes e .
Passo 1
Já que a questão pede para acharmos as componentes, antes de começarmos a desenhar os vetores, vamos lembrar como decompor e achar os valores das componentes de um vetor, beleza?
Nós iremos decompor um vetor em duas componentes, uma na direção do eixo e outra na direção do eixo como na Figura:
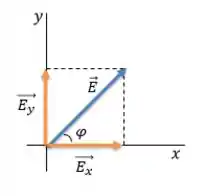
E o valor de cada componente, em função do ângulo fica assim:
A componente que está COlada com o ângulo é igual ao módulo do vetor vezes o COsseno do ângulo. Já a componente que está SEparada do ângulo é igual ao módulo do vetor vezes o SEno do ângulo.
Pegou o macete?
Então agora bora lá desenhar esses vetores e achar as componentes! Vem comigo.
Passo 2
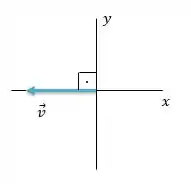
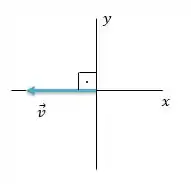
Na figura temos um vetor , ele está no sentido negativo do eixo e, consequentemente, o ângulo que ele forma com o eixo é igual a . Aqui é um pouco mais difícil de ver, mas esse ângulo está colocado com o eixo , show?
Desenho feito! Agora vamos achar o valor das componentes desse vetor. Não esquece o macete ein:
Nota que para a componente tem um sinal de negativo acompanhando. Esse sinal é pra indicar que essa componente está apontando no sentido contrário ao sentido do eixo . Beleza?
A questão nos fornece o módulo do vetor:
E sabemos que:
Então, temos que:
Passo 3
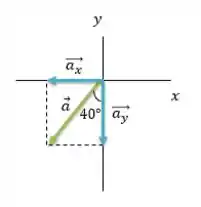
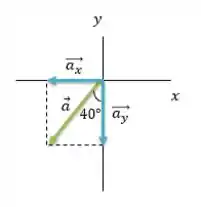
Na figura temos um vetor , ele está à esquerda do semi-eixo negativo e o ângulo que ele forma com esse eixo é igual a . E na Figura também já estão representadas as componentes e desse vetor.
Desenho feito! Agora vamos achar o valor das componentes desse vetor. Não esquece o macete ein:
Nota que para a componente e tem um sinal de negativo acompanhando. Esse sinal é pra indicar que essas componentes estão apontando no sentido contrário ao sentido do eixo e eixo . Beleza?
A questão nos fornece o módulo do vetor:
E temos que:
Então, temos que:
Passo 4
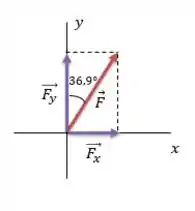
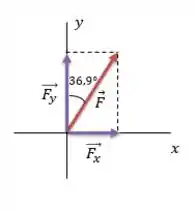
Na figura temos um vetor , ele está à direita do semi-eixo positivo e o ângulo que ele forma com esse eixo é igual a . E na Figura também já estão representadas as componentes e desse vetor.
Desenho feito! Agora vamos achar o valor das componentes desse vetor. Não esquece o macete ein:
A questão nos fornece o módulo do vetor:
E temos que:
Então, temos que:
Resposta
