Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 122

Para fazer um pêndulo, uma bola de 300 g é presa a uma das extremidades de uma corda com 1,4   m de comprimento e massa desprezível. (A outra extremidade da corda está fixa.) A bola é puxada para uim lado até a corda fazer um ângulo de 30,0 ° com a vertical; em seguida (com a corda esticada) a bola é liberada a partir do repouso. Determine (a) a velocidade da bola quando a corda faz um ângulo de 20,0 ° com a vertical e (b) a velocidade máxima da bola. (c) Qual é o ângulo entre a corda e a vertical quando a velocidade da bola é igual a um terço do valor máximo?

Passo 1

(a) Vamos lembrar da lei de conservação de energia:

U 1 + K 1 = U 2 + K 2

Como a bola é liberada a partir do repouso, a energia cinética inicial é K 1 = 0 , então:

U 1 = U 2 + K 2

E já que queremos calcular a velociadde da bola, vamos isolar a energia cinética:

K 2 = U 1 - U 2

K 2 = m g h 1 - h 2

Passo 2

(a) Agora precisamos relacionar a altura com o ângulo que o pêndulo forma com a vertical. Vamos fazer um desenho:

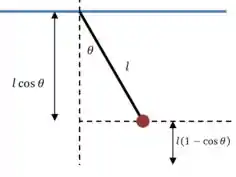
Então a nossa expressão para a energia cinética passa a ser a seguinte:

K 2 = m g h 1 - h 2

K 2 = m g l - cos ⁡ θ 1 + cos ⁡ θ 2

E no primeiro caso temos θ 1 = 30,0 ° e θ 2 = 20,0 ° , então:

K 2 = 0,3 9,8 1,4 - cos ⁡ 30,0 ° + cos ⁡ 20 °

K 2 = 0,303   J

Passo 3

E agora que sabemos a energia cinética, podemos calcular a velocidade:

K 2 = 1 2 m v 2 = 0,303

v 2 = 2 0,303 ( 0,3 )

v = 1,4   m / s

Passo 4

(b) A velocidade máxima da bola acontece quando ela passa pelo ponto mais baixo da trajetória, pois nesse caso toda a energia potencial gravitacional é convertida em energia cinética:

1 2 m v 2 = m g l - cos ⁡ θ 1 + cos ⁡ θ 2

v = 2 g l - cos ⁡ θ 1 + cos ⁡ θ 2

Podemos calcular essa velocidade fazendo θ 1 = 30,0 ° e θ 2 = 0 ° :

v = 2 9,8 1,4 - cos ⁡ 30 ° + cos ⁡ 0 °

v = 1,9   m / s

Passo 5

(c) Queremos encontrar o ângulo no instante em que a velocidade da bola é igual a um terço do valor máximo que acabamos de calcular, ou seja:

v = 1 3 1,9 = 0,64   m / s

Substituindo isso na nossa fórmula de cima com θ 1 = 30,0 ° , ficamos com o seguinte:

v 2 = 2 g l - cos ⁡ θ 1 + cos ⁡ θ 2

0,64 2 = 2 9,8 1,4 - cos ⁡ 30,0 ° + cos ⁡ θ 2

cos ⁡ θ 2 - cos ⁡ 30,0 ° = 0,01489

cos ⁡ θ 2 = 0,8809

θ 2 ≅ 28 °

Resposta

(a) A velocidade da bola quando o ângulo com a vertical mede 20 ° é 1,4   m / s .

(b) A velocidade máxima da bola é v = 1,9   m / s .

(c) A velocidade atinge um terço do valor máximo quando θ = 28 ° .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

E se? Considere a montanha-russa descrita no Problema 52. Por causa de algum atrito entre o carrinho e a pista, o carrinho entra na seção circular com velocidade de 15,0m / s em vez dos 22,0m / s do P
Um carro de montanha-russa mostrado na Figura P7.82 é liberado do repouso de uma altura h e então se move livremente com atrito desprezível. A pista da montanha-russa inclui um giro circular de raio R
Por que a seguinte situação é impossível? Uma atleta testa a força das mãos quando um assistente pendura pesos no seu cinto enquanto ela se pendura pelas mãos em uma barra horizontal. Quando os pesos
Um bloco de massa m 1=20,0k g é conectado a outro bloco de massa m 2=30,0k g por um barbante sem massa que passa sobre uma roldana leve, sem atrito. O bloco de 30,0k g é conectado a uma mola que tem m
Um corpo de 1,00k g desliza para a direita em uma superfície com coeficiente de atrito cinético0,250 (Fig. P7.68a). O corpo tem velocidade de v i=3,00m / s quando faz contato com uma mola leve (Fig. P