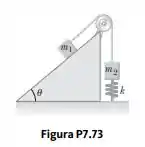
Um bloco de massa é conectado a outro bloco de massa por um barbante sem massa que passa sobre uma roldana leve, sem atrito. O bloco de é conectado a uma mola que tem massa desprezível e uma constante de força , como mostrado na Figura P7.73. A mola é esticada quando o sistema está como mostrado na figura, e o declive não tem atrito. O bloco de é puxado por uma distância para baixo no declive de ângulo (de modo que o bloco de está acima do piso) e liberado do repouso. Encontre a velocidade de cada bloco quando o de está acima do piso (isto é, quando a mola não está esticada).

Passo 1

Resposta