Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 7.Problemas - Ex. 74
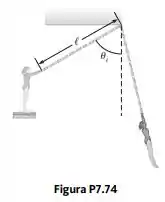
Por que a seguinte situação é impossível? Uma atleta testa a força das mãos quando um assistente pendura pesos no seu cinto enquanto ela se pendura pelas mãos em uma barra horizontal. Quando os pesos chegam a do seu peso corporal, as mãos não aguentam mais seu peso e ela cai no chão. Frustrada por não atingir seu objetivo no teste de força das mãos, ela decide se balançar em um trapézio. O trapézio consiste em uma barra suspensa por duas cordas paralelas, cada uma de comprimento , permitindo que artistas se balancem em um arco vertical circular (Fig. P7.74). A atleta segura a barra e sobe em uma plataforma elevada, começando do repouso com as cordas a um ângulo em relação à vertical. Enquanto ela balança várias vezes para frente e para trás em um arco circular, esquece-se da sua frustração. Suponha que o tamanho do corpo da artista seja pequeno se comparado ao comprimento l e que a resistência do ar seja desprezível.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
A força necessária para se pendurar é igual à força F que a barra do trapézio exerce sobre o atleta. Temos então:
Na parte inferior do balanço, , então:
O atleta não pode sustentar uma tensão de mais de 1.80mg.
Passo 2
O que é a força F na parte inferior do balanço? Para descobrir, aplique a conservação de energia mecânica do sistema atleta-Terra já que o atleta se move entre o ponto inicial e a parte inferior:
na parte inferior.
A tensão na parte inferior é maior do que o atleta pode aguentar; portanto, a situação é impossível.
Resposta
Ver resolução