Repita o problema com o bloco acelerando para cima em um plano inclinado de .

Problema 127: Um bloco de sofre uma aceleração de em uma superfície horizontal sem atrito que faz sua velocidade aumentar de para . Quais são (a) a variação da energia mecânica do bloco e (b) a taxa média com a qual a energia é transferida para o bloco? Qual é a taxa instantânea dessa transferência quando a velocidade do bloco é de (c) e (d) .

E para calcular o ganho de energia potencial gravitacional, precisamos calcular a altura pela qual o bloco se desloca nesse intervalo:

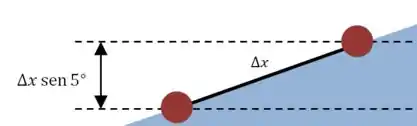
E para calcular , podemos usar a seguinte fórmula:

E então a altura é:

E então o ganho de energia potencial foi:

Então a variação de energia mecânica foi:

(b) Para calcular a taxa média com a qual a energia é transferida para o bloco, temos que calcular quanto tempo passou entre esses dois instantes:

Então:

(c) A taxa instantânea de variação da energia segue essa fórmula aqui:

No nosso problema, a força e a velocidade têm a mesma direção, então esse produto escalar pode ser reescrito da seguinte forma:

Para calcular o módulo da força vamos usar a segunda lei de Newton:

Nesse caso, temos apenas a força empurrando o bloco para cima e a componente do peso puxando para baixo, então:

Então, quando a velocidade do bloco é , a taxa instantânea de transferência de energia é:

(d) Quando a velocidade vale essa mesma taxa é: