Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 11.Problemas - Ex. 1
Um feixe molecular de oxigênio, contendo de velocidade média , incide sobre uma placa segundo um ângulo de com a normal à placa. Calcule a pressão exercida pelo feixe sobre a placa, supondo as colisões perfeitamente elásticas.
Passo 1
Vamos começar relembrando a definição de pressão:
Beleza, a pressão é a razão da força pela área em que essa força age. No nosso caso, a força é produzida pela colisão das moléculas contra a placa.
Podemos calcular essa força pensando na variação de momento de cada molécula:
Vamos fazer um desenho para entender melhor:
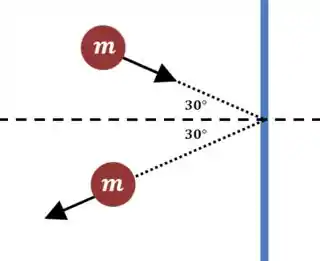
Passo 2
Vamos supor que a velocidade só troca de direção depois da colisão, enquanto o módulo fica igual. Perceba que só a componente horizontal muda!
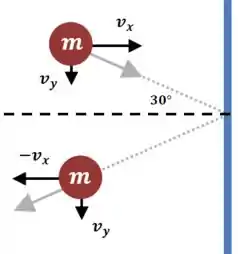
Então a nossa expressão para a variação de momento só precisa considerar o momento na horizontal, e vai ficar assim:
E pela terceira lei de Newton (ação e reação), a variação de momento produzida na parede tem o mesmo módulo e sentido oposto:
E se tivermos partículas colidindo em um intervalo de tempo , a força total é:
Substituindo isso na fórmula da pressão, temos:
Passo 3
Agora vamos tentar reescrever essa expressão usando a densidade que o enunciado deu:
No intervalo de tempo , um feixe de área se movendo com velocidade percorre o seguinte volume:
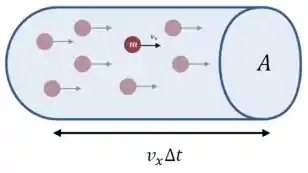
Então:
E substituindo isso na nossa fórmula para pressão:
Como as partículas formam um ângulo de ao colidir contra a parede, a componente horizontal é:
Passo 4
Agora só precisamos substituir os valores numéricos. Precisamos converter a densidade :
E então:
E é a massa de uma molécula de oxigênio (). Como cada átomo de oxigênio tem unidades de massa atômica:
Substituindo:
Resposta
A pressão exercida pelo feixe é de .