Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 100

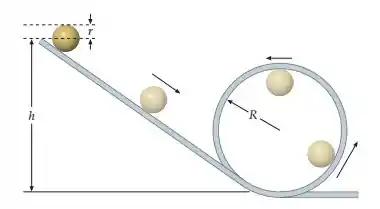
Como engenheiro-chefe de projetos de uma grande fábrica de brinquedos, você deve projetar um brinquedo tipo montanha-russa. A idéia, como mostrada na figura, é que a bolinha de massa m e raio r deve descer rolando um trilho inclinado e percorrer o laço circular que o trilho forma, sem deslizar. A bolinha parte do repouso de uma altura h acima da mesa sobre a qual está o trilho. O raio do laço é R . Determine a menor altura h , em termos de R e de r , para a qual a bolinha permanecerá em contato com o trilho durante todo o percurso. (Não despreze o raio da bolinha em seus cálculos.)

Passo 1

O enunciado diz que depois de escorregar do plano, “a bolinha permanecerá em contato com o trilho durante todo percurso”. Mas, em questões de energia, isso é equivalente a o que? Significa que ela precisa ter energia suficiente para chegar ao ponto mais alto do trilho, e nesse ponto, ele precisa estar prestes a perder contato, ou seja, N = 0 . Então vamos lá fazer as contas e garantir isso.

Passo 2

Conservação de energia:

m g h = m v 2 2 + I ω 2 2 + m g h '

Em que h ' = 2 R - r . Sabemos também que I = 2 5 m r 2 , e como ela rola sem deslizar, v = ω r .

m g h = m v 2 2 + 2 5 m r 2 v r 2 2 + m g 2 R - r

m v 2 2 + m v 2 5 = m g h + r - 2 R

7 10 v 2 = g ( h + r - 2 R )

Passo 3

Já olhamos para a energia, agora vamos para a parte do looping. Para fazer a volta completa com a menor velocidade possível, no ponto mais alto a bola está prestes a perder contato com a superfície, ou seja, N = 0 :

F c p = N + m g ≅ m g

m v 2 R - r = m g

v 2 = g ( R - r )

Passo 4

Substituindo na equação da energia:

7 10 g R - r = g h + r - 2 R

7 R - 7 r = 10 h + 10 r - 20 R

10 h = 27 R - 17 r

h = 2.7 R - 1.7 r

Resposta

h = 2.7 R - 1.7 r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que
67 . || Um bloco de 3,0k g é preso a um barbante que é enrolado ao redor de um cilindro oco de 2,0k g e 4,0c m de diâmetro, que pode girar livremente. (Use a F i g u r a12.34 , mas considere o cilindr
A F I G U R AP D 12.92 mostra um pedaço triangular de queijo suíço em pé sobre uma tábua de queijos. Você e seus colegas estão se perguntando sobre o que acontecerá se você for inclinando lentamente a
96 . Um professor de física encontra-se em pé, em repouso, sobre uma plataforma giratória de 5,0k g e 50c m de diâmetro capaz de girar sem atrito. Seu ajudante possui uma roda de bicicleta com 64c m d
93 . || Um cubo de massa m desliza sem atrito com velocidade v 0 . Ele, então, sofre uma colisão perfeitamente elástica com a extremidade inferior de uma haste de comprimento d e massa M = 2 m . A has