Uma bola de boliche, de massa e raio , é lançada de forma que, ao atingir o piso, está se movendo horizontalmente com um rapidez , sem girar. Ela desliza uma distância durante um tempo antes de começar a rolar sem deslizar. (a) Se é o coeficiente de atrito cinético entre a bola e o piso, determine , e a rapidez final da bola. (b) Determine a razão entre a energia cinética final e a energia cinética inicial da bola. (c) Determine , e para e .
Passo 1
a) Oláaa, querido! Cê está bem? O que acontece aqui é que a bola desliza até que a velocidade dela seja , e nesse instante ela começa a rolar sem deslizar.
Queremos saber o tempo que esse movimento de deslizamento leva, a velocidade e a distância percorrida. E para achar essas coisas, a gente precisa da aceleração do centro de massa da bola nesse período e a aceleração angular que ela vai adquirir.
Se precisa achar aceleração e há ação da força de atrito cinético na situação (como o enunciado fala) é maneiro usar a segunda lei de Newton. E falou de usar a segunda lei de Newton, a gente pensa logo em fazer os diagramas de corpo livre da esfera (bola). Fica assim:
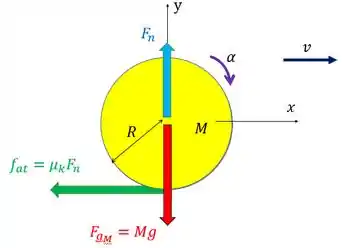
Obs: esse exercício é bem parecido com o exemplo 9-19. Se depois quiser ver como o livro resolve, a gente deixa aqui essa dica para te ajudar, tá?
Passo 2
Vamos começar por .
No eixo , pela segunda lei de Newton:
Sendo que é a força de atrito cinético entre o piso e a bola:
Só que a gente não sabe quem é . Vamos achar ela pela 2ª lei de Newton na direção :
Como não tem movimento nessa direção, :
Daí substituindo na equação do eixo :
Ela é negativa porque vai desacelerar a bola.
Passo 3
Agora vamos achar para quando a bola começa a girar. Como a aceleração do centro de massa que a gente achou é para o momento com deslizamento, não podemos dizer que .
E como a gente faz então? Cara, a gente pode usar a segunda lei de Newton para a rotação, já que agora estamos com a bola girando.
Ela tem essa cara:
A única força que não passa pelo centro da bola é . Então ela é a única que vai gerar torque. E como e são perpendiculares, o torque é dado por :
Vimos que e é o momento de inércia de uma esfera em relação a um eixo passa pelo seu centro e vale . Substituindo essas duas coisas:
Isolando quem a gente quer
Passo 4
Agora a gente pode achar o que ele pede. Como? Bem, é a velocidade da bola quando ela começa a rolar sem deslizar, certo? Então ela pode ser escrita como:
Então a gente precisa da rapidez angular da bola. Como a gente tem , e sabe que a rapidez angular inicial é nula no momento inicial (não temos rolamento em ). Podemos usar essa equaçãozinha para achar :
Já que ,
Mas a gente também pode escrever usando as equações da cinemática linear já que temos . Temos:
Subsituindo a nossa expressão de :
Igualando essas duas expressões para :
Isolando
Esse é o tempo do período com deslizamento!
Passo 5
Temos a expressão da velocidade final:
Substituindo a expressão que a gente achou de :
E a distância percorrida pode ser achada por essa equação para aceleração constante:
Substituindo nossas expressões para e :
Nossa, que trabalheira! Mas calma que não acabou ainda...
Passo 6
b) O momento final é quando a bola começa a rodar sem deslizar. Então nesse instante a bola tem energia cinética dividida em translacional (do movimento linear) e rotacional (porque gira):
Substituindo as expressões de cada uma:
Onde é a rapidez do centro de massa da bola (que é uma esfera), com que ela se move pelo piso.
E lembra que é o momento de inércia da esfera (a bola) em relação ao seu centro (eixo de rotação) e vale . E como não há deslizamento, a gente pode escrever a rapidez angular usando essa expressão:
Substituindo as nossas expressões de e em :
Passo 7
A energia inicial é quando ela começa a deslizar com velocidade inicial . A energia cinética nessa situação é só a de translação:
Aí a razão entre a energia final e inicial é:
Passo 8
c) Substituindo os valores do enunciado nas expressões encontradas na letra (a):
Resposta
- , ,
- , ,