Na Fig. 21-27 a, as partículas e têm uma carga de cada uma e estão separadas por uma distância . (a) Qual é o módulo da força eletrostática que a partículaexerce sobre a partícula ? Na Fig. 21-27 b, a partícula , com uma carga de , é posicionada de modo a completar um triângulo equilátero. (b) Qual é o módulo da força eletrostática a que a partícula é submetida devido à presença das partículas e ?

O item a) não tem mistério para se resolver, é pedido pra encontrarmos a força que a partícula 2 exerce sobre a partícula 1, se liga no esquema.

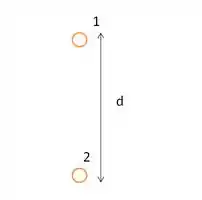
Para calcularmos a força que exerce sobre , basta a gente usar a fórmula da força eletrostática:

E aí substituímos os valores de e :

Pra resolver os outros itens vamos precisar analisar a geometria do problema e aí encontraremos a força total, beleza?

Agora ficou mais divertido! O item b pede a força total sobre a partícula 1 e a força sofrida pela partícula 1 é igual a soma das forças eletricas que cada partícula exerce sobre ela (principio da superposição).

Aqui a gente vai ter que brincar um pouquinho com a geometria do problema, se liga no desenho.

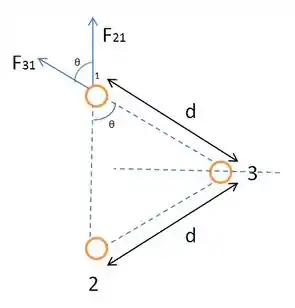
A força é a força que a partícula 2 faz na partícula 1, enquanto a força é a força que a partícula 3 faz na partícula 1.

Como foi dito no texto, o triângulo formado é equilátero, ou seja, todos os seus lados são iguais e os ângulos internos são iguais a 60°.

Se é um triângulo equilátero as partículas estão equidistantes ou seja:

E aqui se liga, vamos calcular a força que a partícula 3 exerce na partícula 1.

E nós já tínhamos calculado a força da partícula 2 em 1 e ela era igual a:

Tranquilo até aqui? 😊

Como já vimos, esses dois vetores possuem o ângulo entre eles, e também já sabemos que esse ângulo vale 60°, pois ele é igual ao ângulo interno de um triângulo equilátero. Logo, podemos calcular o módulo da soma dos dois vetores:

Substituindo nossos valores:

E aí! O que achou? Responde Aí! 😁