Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 23.Questionário - Ex. 14

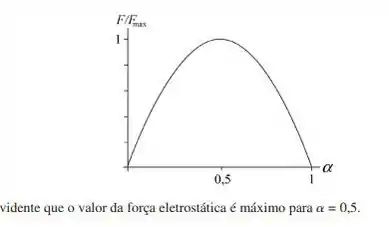
Da carga Q que está presente em uma pequena esfera, uma fração α é transferida para uma segunda esfera. As esferas podem ser tratadas como partículas. (a) Para que valor de α o módulo da força eletrostática F entre as duas esferas é o maior possível? Determine (b) o menor e (c) o maior valor de α para o qual F é igual a metade do valor máximo.

Passo 1

E aí galerinha, vamos destruir essa questão comigo? Vamos láaaa!

As cargas das duas esferas são q = α Q (em que α é um número maior que 0 e menor que 1) e Q - q = ( 1 - α ) Q . De acordo com a Eq. 21-1, temos:

F = 1 4 π ϵ 0 ( α Q ) [ ( 1 - α ) Q ] d 2 = Q 2 α ( 1 - α ) 4 π ϵ 0 d 2

O gráfico a seguir mostra a força normalizada  F / F m a x  em função de  α , em que  F m a x = Q 2 / 16 π ε 0 d 2 .

(a) É evidente que o valor da força eletrostática é máximo para  α = 0,5 .

Passo 2

(b) Fazendo  F = F m a x / 2 , obtemos:

Q 2 α ( 1 - α ) 4 π ϵ 0 d 2 = Q 2 32 π ϵ 0 d 2

que nos dá, depois de algumas manipulações algébricas, a equação do segundo grau

α 2 - α + 1 8 = 0

cujas raízes são

1 2 1 + 2 2  e  1 2 1 - 2 2

Passo 3

(c) O menor valor de α é α = 1 2 1 - 2 2 ≈ 0,15 .

Opa, gostou da resolução? Responde Aí!

Passo 4

(d) O maior valor de  α  é  α = 1 2 1 + 2 2 ≈ 0,85 .

Opa, gostou da resolução? Responde Aí!

Resposta

a. α = 0,5

b. 1 2 1 + 2 2  e  1 2 1 - 2 2

c. 0,15

d. 0,85 .

Exercícios de Livros Relacionados

21.17 Três cargas puntiformes estão dispostas ao longo do eixo x . A carga q 1=+ 3,0µ C µ está na origem e a carga q 2=- 5,0µ C µ está em x = 0,200m . A carga q 3 = -8,0 µ C µ . Onde q 3 estará locali
Três cargas puntiformes estão dispostas ao longo do eixo X a carga Q 1=+3,0μ C está na origem e a carga Q 2=- 5,0μ C está em x=0,200m . A carga Q 3=+8,0μ C , onde que Q 3 estará localizado quando a fo
Em uma nuvem de tempestade, pode haver cargas elétricas de + 40,0C próximas ao topo da nuvem e – 40,0C na parte inferior. Essas cargas são separadas por 2,00k m . Qual é a força elétrica sobre a carga
Na Fig. 21-27a, a partícula 1 (de carga q 1 ) e a partícula 2 (de carga q 2 ) são mantidas fixas no eixo x , separadas por uma distância de 8,00c m . A força que as partículas 1 e 2 exercem sobre uma
Na Fig. 21-31, as partículas 1 e 2 , de carga q 1=q 2=+3,20 × 10 - 19C , estão no eixo y , a uma distância d=17,0c m da origem. A partícula 3 , de carga q 3=+ 6,40 ×10 - 19 C , é deslocada ao longo do