Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 25.3 - Ex. 14
Na Fig. 25-30, a bateria tem uma diferença de potencial V = 10,0 V e os cinco capacitores têm uma capacitância de 10,0 μF. Determine a carga (a) do capacitor 1; (b) do capacitor 2.
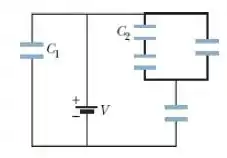
Passo 1
É isso galerinhaaa, animados para mais uma ?!
Vamos melhorar o nosso desenho:
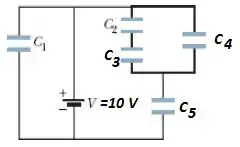
Boom, para calcular a carga de um capacitor não tem mistério, é só usar uma fórmula bem tranquilinha:
O problema nos disse que:
Para o capacitor 1 nós só precisamos substituir os dados na fórmula, não tem mistério:
Já achamos a letra (a), agora o que nos resta é achar a (b) !!
Passo 2
Na letra (b) o buraco em mais em baixo porque os capacitores estão em série e em paralelo, tá uma misturebaa !!
Quando nós temos este caso precisamos achar a capacitância equivalente, bora ver?
Os capacitores 2 e 3 então em série, e neste caso a capacitância equivalente será:
Agora e estão em paralelo, quando isso acontece a capacitância equivalente é calculada como:
Mas ainda tem um capacitor sobrando ali, não é?
E ele está em série com
Agora podemos achar a carga que passa por este capacitor equivalente que acabamos de achar usando a fórmula do Passo 1:
Nós achamos a carga equivalente, mas na verdade queremos somente a carga que passa em 2, certo?
Então faremos algo tipo um caminho inverso, tudo bem?
O capacitor e estão em série, por isso o potencial não é o mesmo, mas a carga permanece a mesma!! Sendo assim nós vamos usar a fórmula da carga para achar o novo potencial:
Como e estão em série, a nova tensão será dividida igualmente entre eles, então a tensão que passa pelo capacitor 2 será:
Agora sim nós podemos achar a carga que passa pelo capacitor 2, porque já sabemos que:
Então:
Nada complicado, não é? Muitos detalhes, mas quanto mais vocês praticarem mais fácil vocês acharão !!
Resposta
(a)
(b)