Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.5 - Ex. 34
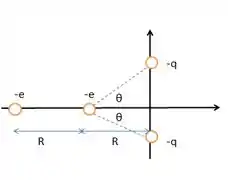
A Fig. 21-34 mostra dois elétrons, e , no eixo e dois íons, e , de carga , no eixo . O ângulo é o mesmo para os dois íons. O elétron está livre para se mover; as outras três partículas são mantidas fixas a uma distância horizontal do elétron e seu objetivo é impedir que o elétron se mova. Para valores fisicamente possíveis de , determine (a) o menor valor possível de ; (b) o segundo menor valor possível de ; (c) o terceiro menor
valor possível de .
Passo 1
E aí, galerinha! 😁
Nesse problema temos dois elétrons, e , no eixo e dois íons, e , de carga , no eixo . O ângulo é o mesmo para os dois íons. O elétron está livre para se mover e as outras três partículas são mantidas fixas a uma distância horizontal do elétron e nosso objetivo é impedir que o elétron se mova.
Pra isso temos que encotrar o menor, o segundo menor e o terceiro menor ângulo em que isso acontece.
Tem ideia de como fazer isso? 🤔
Uma dica importante para resolver problemas como esse é verificar se existe simetria no problema. Nesse caso, existe simetria com relação ao eixo . Então a força na direção é nula.
Então, a força total só é devida à componente , sendo nula na condição de equilíbrio, ocorre que:
Veja só! 😁
Passo 2
Pela regra do cosseno, temos que
Substituindo em
Ou seja:
Então:
Sendo , pois toda carga elétrica é um mútiplo inteiro da carga elementar, a gente tem que:
Sendo um número inteiro.
Tranquilo até aqui? 😁
Passo 3
Nesse caso, isolando em um lado da igualdade, temos
O menor valor de nesse caso corresponde ao menor valor inteiro de :
O segundo menor valor de corresponde a :
E o terceiro menor valor de corresponde a :
E aí! O que achou? Responde Aí! 😉
Resposta
- 0,988 rad