Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.5 - Ex. 30
A Fig. 21-33a mostra duas partículas carregadas, e , que são mantidas fixas em um eixo x. O valor absoluto da carga da partícula é . A partícula , de carga , que estava inicialmente no eixo , nas vizinhanças da partícula , é deslocada no sentido positivo do eixo .
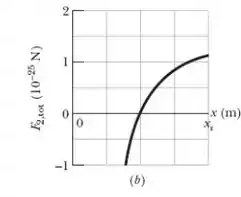
Em consequência, a força eletrostática total a que está sujeita a partícula varia. A Fig. 21 -33b mostra a componente da força em função da coordenada da partícula . A escala do eixo é definida por . A curva possui uma assíntota para . Determine o valor da carga da partícula , em unidades de , incluindo o sinal.
Passo 1
Fala galerinha, sei que esse enunciado é um pouco grande e confuso mas vou tentar traduzir tudo o que ele quer na nossa língua, beleza?
Ele deu o módulo das cargas e deu também o sinal de sendo positiva. E quer saber de nós o valor da carga e também o seu sinal. Para nos ajudar foi dado um gráfico da força em função da posição da carga .
Para resolver isso a gente vai usar a equação da força elétrica:
E o gráfico dado pela questão.
Veja só! 👀
Passo 2
Vamos analisar o gráfico ali, disseram pra gente que o valor de era 0,8 então na metade desse temos um ponto importante que é onde a força é zero.
O que isso quer dizer? Como a força pode ser zero ali? Bem, temos duas cargas atuando em cima da carga , sendo assim a força eletrostática vai ser.
No ponto em que temos a força é zero.
Podemos dividir os dois lados por e por :
Analisando essa brincadeira aí em módulo temos que e portanto . Já o sinal da carga pela equação precisa ser negativo ou não poderíamos zerar essa equação e assim.
Tranquilo até aqui? 😬
Passo 3
Agora, veja o que acontece quando a distância aumenta muito.
Quando a parcela da combinação tende 0. E a força fica com essa cara:
e, então
Se isolarmos a carga da equação, teremos:
E aí! o que achou? Responde Aí! 😎
