Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.7 - Ex. 40

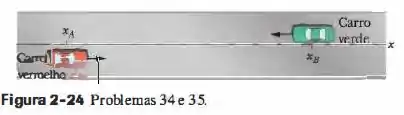
Na Fig. 2-24, um carro vermelho e um carro verde, iguais exceto pela cor, movem-se um em direção ao outro em pistas vizinhas e paralelas a um eixo x . No instante t   = 0 , o carro vermelho está em x A = 0 e o carro verde está em x B = 220   m . Se o carro vermelho tem uma velocidade constante de 20   k m / h , os carros se cruzam em   x   = 44,5   m ; se tem uma velocidade constante de 40   k m / h , os carros se cruzam em x = 76,6   m . Quais são (a) a velocidade inicial e (b) a aceleração do carro verde?

Passo 1

Pessoal, se o carro vermelho tem uma velocidade v 1 = 20 k m / h = 5 , 5 6 m / s , ele se encontra com o carro verde quando se desloca Δ x 1 = 44,5 m e faz isso em um tempo:

t 1 = Δ x 1 v 1 = 44,5   m 5 , 5 6   m / s = 8,0   s

No caso que o carro vermelho tem uma velocidade v 2 = 40 k m / h = 11 m / s , ele se encontra com o carro verde quando se desloca Δ x 2 = 76,6 m e faz isso em um tempo:

t 2 = Δ x 2 v 2 = 76,6   m 11,1   m / s = 6,9   s

Passo 2

Agora que já sabemos cada intervalo de tempo, vamos substituir todas as informações que temos na função horária da posição para o carro verde nas duas situações dadas.

x = x 0 + v 0 t + a t 2 2

45,5 = 220 + 8 . v 0 + a . 8 2 2 → v 0 = - 175,5 - 3 2 . a 8

Podemos usar esse resultado de v 0 para substituir na equação de quando v = 11 m / s .

76,6 = 220 + 6,9 . v 0 + a . 6,9 2 2

76,6 - 220 = 6 , 9 . ( - 175,5 - 32 . a 8 ) + 2 3 , 8 . a

- 143,4 = - 151 , 4 - 27,6 . a + 23,8 . a

- 143,4 + 151,4 = - 27,6 . a + 23,8 . a

8 = - 3,8 . a → a = 8 - 3,8

a = - 2,1   m / s 2

Passo 3

Para encontrar v 0 é só substituir o valor de a na expressão que encontramos para v 0 .

v 0 = - 175,5 - 32 . a 8 = - 175,5 - 32 . ( - 2,1 ) 8

v 0 = - 13,5   m / s

Resposta

a) - 13,5   m / s

b) - 2,1   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motorista possui tempo de reação de 0,50s , e a desaceleração máxima que seu carro atinge é de 6,0m / s 2 . Ele está dirigindo a 20m / s quando, subitamente, vê um obstáculo na estrada 50m à frente
Suponha que eu esteja dirigindo a 20m / s enquanto tento trocar o CD e não presto atenção no que me cerca. Quando olho de volta para a frente, descubro-me a 45 m do cruzamento com uma ferrovia. Sem to
Você está dirigindo em uma rodovia tarde da noite quando um veado para no meio da estrada 35m à sua frente. Seu tempo de reação antes de acionar os freios é de 0,50s , e a desaceleração máxima de seu
a) Em unidades do SI, que aceleração constante um carro deve desenvolver a fim de passar de zero a 100k m / h em 10s ? b) A que fração de g isso corresponde? c) Que distância o carro terá percorrido q
a) Quantos dias levará para uma espaçonave acelerar até a velocidade da luz ( 3,0 × 10 8m / s ) com aceleração igual a g ?b) Que distância ela percorrerá neste intervalo?c) A que fração de ano-luz cor