Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.8 - Ex. 33

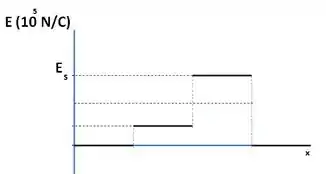
A Fig. 23-42a mostra três placas de plástico de grande extensão, paralelas e uniformemente carregadas. A Fig. 23-42b mostra a componente x do campo elétrico em função de x . A escala do eixo vertical é definida por E   =   6,0 × 10 5     N / C . Determine a razão entre a densidade de cargas na placa 3 e a densidade de cargas na placa 2 .

Passo 1

Primeiro, vamos olhar pra região entre as placas 1 e 2 . Lembre que o campo elétrico devido a uma placa infinita positivamente carregada aponta para fora dela dessa forma:

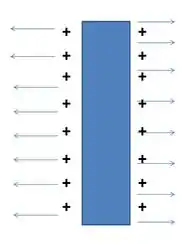
Sendo assim, a gente tem que, na região entre a origem e 1 :

E 01 = - E 1 - E 2 - E 3 = 0

Passo 2

Agora, bora olhar pra região entre 1 e 2 :

E 12 = E 1 - E 2 - E 3 = 2 × 10 5 N / C

Passo 3

Na região entre 2 e 3 :

E 23 = E 1 + E 2 - E 3 = 6 × 10 5 N / C

Passo 4

Subtraindo as equações dos passos 2 e 3 :

4 × 10 5   N / C = 2 E 2

Então:

E 2 = 2 × 10 5 N / C

Agora, usando a equação do passo 1 e a do passo 2 , temos:

E 1 + E 3 = - 2 × 10 5 N C

E 1 - E 3 = 4 × 10 5 N C

Então:

E 1 = 1 × 10 5 N C

e

E 3 = - 3 × 10 5 N C

Passo 5

A gente tá quase lá!

Agora, pra gente saber a razão entre as densidades de carga nas placas 3 e 2 , basta dividirmos os campos elétricos que encontramos acima, já que, pra um plano infinitamente carregado com uma densidade superficial uniforme de carga σ , E = σ ϵ 0 .

σ 3 σ 2 = E 3 E 2 =   - 3 2 = - 1,5

Resposta

- 1 , 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera dentro de uma esfera. Uma esfera condutora sólida de raio a possui carga q . Ela está no interior de uma esfera condutora oca concêntrica com raio interno b e raio externo c . A esfera cond
Um cilindro sólido muito longo de raio R possui uma distribuição uniforme de carga positiva, sendo ρ a carga por unidade de volume. a Deduza uma expressão para o campo elétrico no interior do volume,
O cabo coaxial. Um cabo coaxial longo é constituído por um cilindro interno condutor de raio a e por um cilindro externo coaxial com raio interno b e raio externo c . O cilindro externo está apoiado e
Um tubo cilíndrico condutor muito longo (cilindro oco) possui raio interno a e raio externo b . Ele possui carga por unidade de comprimento igual a + α , em que α é uma constante positiva com unidades
Um cilindro circular muito longo, de raio R , está uniformemente carregado, com densidade volumétrica de carga δ .Por argumentos de simetria (explicando-os), obtenha a direção e o sentido do campo E →