Um tubo cilíndrico condutor muito longo (cilindro oco) possui raio interno e raio externo . Ele possui carga por unidade de comprimento igual a , em que é uma constante positiva com unidades de . Um fio carregado está sobre o eixo do tubo. O fio possui uma carga por unidade de comprimento igual a . Determine o campo elétrico em função de e da distância ao eixo do tubo para ; ; . Mostre seus resultados em um gráfico de em função da distância . Qual é a carga por unidade de comprimento sobre a superfície interna do tubo; a superfície externa do tubo?
Passo 1
Supondo uma superfície gaussiana cilíndrica de raio e comprimento com o mesmo eixo que o tubo e o fio, temos que o seu campo elétrico será dado através da carga por unidade de comprimento que está em seu interior por causa do cilindro interno. Então, usando a equação do campo elétrico para uma linha infinita, teremos:
Passo 2
Agora, consideramos uma superfície gaussiana cilíndrica com raio , ela irá envolver apenas o fio carregado e terá a mesma densidade linear que o fio. Logo, o campo elétrico dessa superfície será:
Para uma superfície gaussiana que esteja na região dentro do tubo cilíndrico, lembramos que o campo elétrico no interior de um condutor carregado é nulo. Então, o campo para é igual a zero.
O último caso considera uma superfície gaussiana cilíndrica de raio que envolver tanto o fio carregado quanto o tubo. Dessa forma, ele irá possuir uma carga por unidade de comprimento que é o resultado da soma das cargas dos dois corpos. Logo, seu campo elétrico é:
Passo 3
O gráfico que mostra esses resultados está mostrado a seguir:
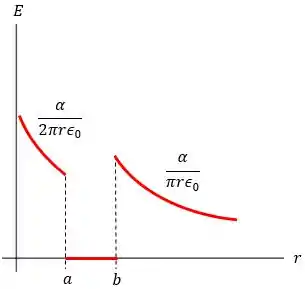
Passo 4
Para calcular a carga por unidade de comprimento da superfície interna do tubo, podemos considerar uma superfície gaussiana cilíndrica que se encontre nessa região, ou seja, tenha raio tal que .
Essa superfície contém em seu exterior a densidade linear do fio e, como o seu campo elétrico é nulo, a densidade no seu interior deve ter mesma intensidade e sinal oposto () a fim de anular o campo elétrico na superfície.
Já para a superfície externa do tubo, usando uma superfície gaussiana cilíndrica com que envolve tanto o tubo quanto o fio, então ela envolve a densidade linear do tubo e do fio. Logo, ela possui carga por unidade de comprimento