Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 42

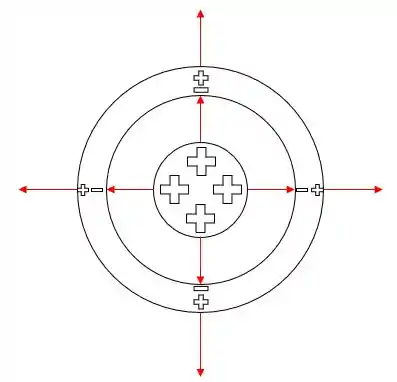
Uma esfera dentro de uma esfera. Uma esfera condutora sólida de raio a possui carga q . Ela está no interior de uma esfera condutora oca concêntrica com raio interno b e raio externo c . A esfera condutora oca não possui nenhuma carga líquida. a Deduza uma expressão para o módulo do campo elétrico em função da distância r ao centro para as regiões r < a , a < r < b , b < r < c , e r > c . b Faça um gráfico do módulo do campo elétrico em função da distância r , de r = 0 até r = 2 c . c Qual é a carga sobre a superfície interna da esfera oca? d Qual é a carga sobre a superfície externa da esfera oca? e Represente as cargas da pequena esfera usuando quatro sinais de adição. Faça um esboço das linhas de campo do sistema no interior de um volume esférico de raio igual a 2 c .

Passo 1

Para saber o campo elétrico em cada situação, precisamos considerar uma superfície gaussiana adequada para cada uma delas.

Primeiramente, supondo uma superfície gaussiana esférica de raio r < a , temos que o seu campo elétrico será é nulo por ser um condutor sólido carregado e não possuir carga em seu interior.

O mesmo ocorre para uma superfície gaussiana que tenha raio b < r < c , visto que nessa região ela se encontra no interior da esfera oca que também é um condutor sólido carregado.

Já para a superfície gaussiana de raio a < r < b , ela envolve a carga da esfera mais interna com valor + q . Logo, o seu campo elétrico será dado por:

E = k q r 2

Tomando a superfície de raio r > c , a única carga envolvida por ela também é a da esfera mais interna e, logo, possui o mesmo valor de campo elétrico:

E = k q r 2

Passo 2

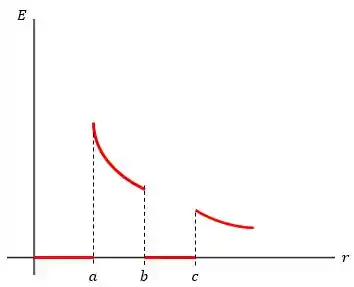
O gráfico deste caso pode ser dado por:

Passo 3

Na região da superfície interna da esfera oca, ou seja, em b < r < c , por se tratar de um condutor carregado, o campo elétrico deve ser nulo.

Como a superfície gaussiana nesta região envolve a carga + q da esfera condutora, então a carga na superfície deve ser - q . Consequentemente, na superfície interna da esfera oca a carga é - q .

Passo 4

Agora, como a esfera oca não possui carga líquida e, logo, não apresenta fluxo elétrico por ela, tendo uma carga - q na superfície interna, a carga na superfície externa deve ter mesma intensidade e sentido contrário para que haja essa “anulação” e a carga resultante seja zero na superfície. Logo, a superfície externa tem carga + q .

Passo 5

O esboço das linhas do campo elétrico e dos sinais das cargas é dado a seguir:

Resposta

a   r < a → E = 0

a < r < b → E = k q r 2

b < r < c → E = 0

r > c → E = k q r 2

c - q

d + q

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Num trabalho escrito em 1911, Ernest Rutherford disse: “Para se ter alguma ideia das forças necessárias para desviar uma partícula α através de um grande ângulo, considere um átomo contendo uma carga
Mostre que o equilíbrio estável é impossível se as únicas forças atuantes forem forças eletrostáticas. (Sugestão) Suponha que uma carga + q fique em equilíbrio estável ao ser colocada num certo ponto
A Eq. 25-12 E = σ ϵ 0 nos dá o campo elétrico para pontos próximos de uma superfície condutora carregada. Aplique-a a uma esfera condutora de raio r e carga q , e mostre que o campo elétrico fora da e
Um próton descreve um movimento circular com velocidade escalar v = 3,00 × 10 5 m / s ao redor e imediatamente fora de uma esfera carregada, de raio r = 1,00c m . Qual é a carga sobre a esfera.
Uma esfera maciça, não condutora, de raio R , tem uma distribuição de carga não uniforme de densidade volumétrica dada por ρ = ρ 1 r R , onde ρ 1 é uma constante e r é a distancia ao centro da esfera.